词(Word)
对于人类所理解的词语,英文单词(比如apple)为一个词,中文里一个字(中)或者一个词语(苹果)为一个词。
1 词向量(Word Vector)
1.1 词向量简介
词向量也叫做词嵌入(Word Embedding),将人类所理解的自然语言的词映射为实数向量,也就是将文本中的词转换为数字向量的方法。一般情况下是将一个单词用高维的向量来表示,例如:
"狗"表示为[2, 3, 3]
"猫"表示为[1, 2, 3]
"雪"表示为[14, 2, 1]
1.2 词向量相似性度量
对于上述三个词向量,常见的方法是使用余弦相似度来计算词向量之间的距离:
狗和猫的余弦相似度: \[ cos(\theta_1) = \frac{2\times1+3\times2+3\times3}{\sqrt{2\times2+3\times3+3\times3}\sqrt{1\times1+2\times2+3\times3}} = 0.969 \]
狗和雪的余弦相似度为: \[ cos(\theta_2) = \frac{2\times14+3\times2+3\times1}{\sqrt{4+9+9}\sqrt{196+4+1}} = 0.556 \]
两个向量之间的夹角\(\theta\)越小,两个向量靠的越近,通过比较向量之间夹角的余弦值的大小(夹角越小,余弦值越大)判断向量之间的相似性也就是词之间的相似性。
再举例来看,假设Agriculture文档和History文档与词disease的共现次数分别为20、30,与词eggs的共现次数分别为40、20,在二维坐标中显示如下图,同时计算Agriculture和History对应的两个向量之间的余弦相似度。
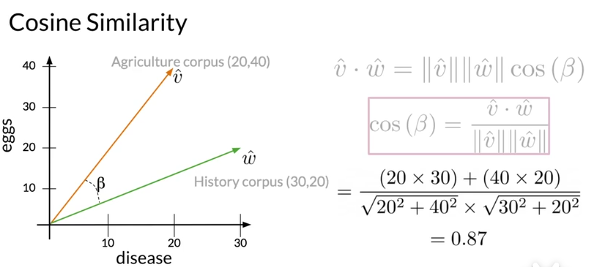
此外还可以用欧式距离等来计算向量之间的距离(相似性)。距离来看,假设文档A为娱乐文档(Entertainment),文档B为机器学习文档,它们与film的共现次数分别为7000、1000,与data的共现次数分别为500、9320,放在二维坐标中如下图所示,计算两者之间的欧式距离可以表示两者之间的相似性。
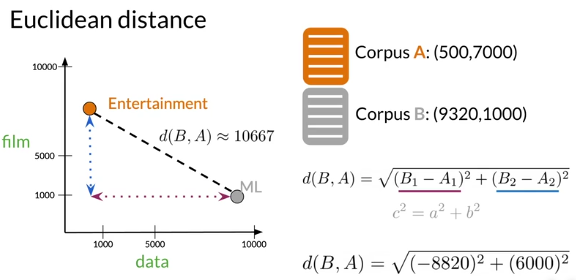
1.3 词的编码演变
词向量(Word Embedding)
上世纪五十年代语言学家Joos、Harris、Firth等人提出了分布式假说:出现在相似语境的词往往有相似的含义。将一个词用它的上下文来表示的分布式词向量表现形式脱颖而出。用一个简单的例子来解释:
啊,今天天气真好啊! 真开心,今天遇到的人都超好。
啊,今天的天气非常棒啊! 真开心,今天遇到的人都非常棒。
在众多的语句当中只选上面各两个句子,通过很多类似的句子的学习,好和棒拥有十分相近的含义,因为它们有十分相近的上下文。(在我们看来更是如此,好和棒的意思十分接近。)
在词向量出现之前的一些编码:
One-Hot编码
最早的对此进行编码的方式是One-Hot,对所有词进行一位有效位编码,即在向量中只有一个位置为1其余所有位置为0。
例如下面对apple、bag、cat等的编码:

one-hot编码的问题在于世界上的词太多太多了,这让向量的长度十分长,而且one-hot编码的词无法表现出不同词之间的相似性(词向量之间的余弦值恒为0)。
Word Class
既然one-hot没办法拥有不同词直接的关系,Word Class就是将不同的词进行分类,这样词之间的关系就比较明了了。
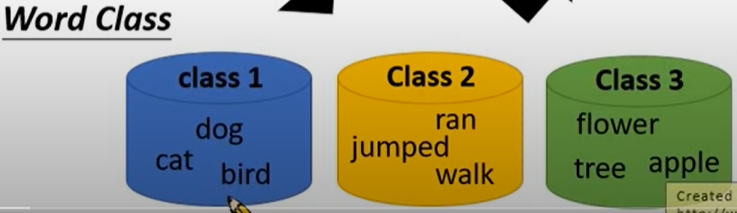
Word Class虽然有效的表示了不同词的类别,但是如何分类是个很大的问题。
1.4 词向量的运算
通过对词向量的运算,我们可以做出一定的推理,如下图中问题: 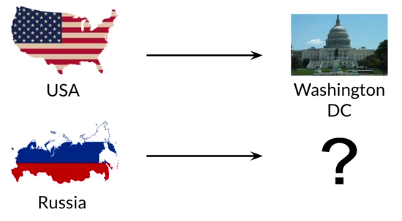
现有拥有一个假设的二维向量空间,在其中不同的国家和首都有不同的向量表示: 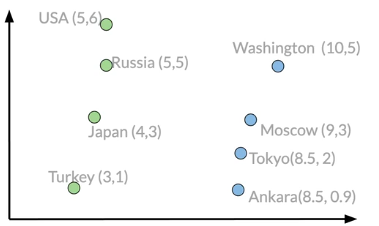
已经知道USA的首都是Washington,两者之差的向量[5 -1]如下图所示,对于Russia,加上[5 -1]就可以大致得到它的首都的向量[10 4],通过对比向量相似度发现[9 3]也就是Moscow是其首都。 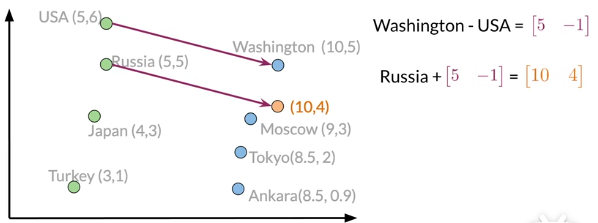
通过对词向量的不同运算可以得到我们想要的结果,也就是通过已知的其他词向量之间的关系进行预测。
关于词向量的运算更详细的实验见另一篇博客传送门。
2 词嵌入(Word Embedding)方法
1 TF-IDF
TF-IDF(Term Frequency-Inverse Document Frequency),是一种统计方法,基于信息检索(Information Retrieval, IR)进行的。首先来看最简单的基于IR的方式:worf-word matrix(词-词矩阵)
word-word matrix
首先我们确定好初始的word-word matrix,它的一行代表一个目标词,列代表上下文的词,确定好所有的行和列,然后在训练的语料库中进行统计,使用一定大小的窗口(2或3或4等都可以)统计目标词(对应行)上下文的词(对应列)出现的次数。
统计时对目标词所使用的窗口是指统计目标词左边多少词右边多少词,例如窗口为2代表检索时只看中心词左边两个个和右边两个词,见下图(来自Stanford的CS224N课PPT)。
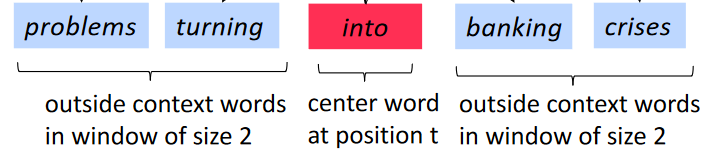
现在来看在维基百科语料库中进行统计得到的word-word矩阵(来自《Speech and Language Processing》一书的pdf,希望它尽快写完出版),选取很小的一部分,包含cherry,strawberry,digital,information四个word:

目标词digital用红色标注的行向量来表示,可以看出digital和information拥有比较相近的上下文表示(向量靠的近)。
word-word matrix还是存在一些问题,像the,that,it等高频出现的无意义的词会影响其他频率出现少但是和中心词有实在联系和意义的词。这就出现了一个悖论:频繁出现在中心词附近的词能够代表中心词的语境,比出现次数少的词重要;但,频繁出现在中心词附近的普遍出现的词(像the这种)又是不重要的,无法代表中心词的含义、语境。TF-IDF的方法就平衡了上述悖论的冲突。
TF-IDF
TF-IDF所利用的思想是如果某个词在一篇文章中出现的频率高并且在其他文章中出现的次数比较少,那么这个词就适合用来区分。TF-IDF是TF(词频)和IDF(逆向文章频率)的乘积。
- TF(词频)
TF(词频)就是一个词t(当前的词记为t)在文章d中出现的频率(次数),可以记为: \(tf_{t,d} = count(t, d)\) 可以对上述词频进行一下压缩,也就是对\(tf_{t,d}\)取对数(\(log_{10}\)),为了防止有些词的出现次数为0导致无法取对数,所以对统计的次数全部加1: \(tf_{t,d} = log_{10}(count(t,d) + 1)\)
有时为了防止词频偏向长的文章,通常会将tf-{t,d}进行归一化,就是增加一个文章d中全部的词出现的次数的分母(即除以文章的总次数)。
- IDF(逆向文章频率)
IDF就是为了让仅仅出现在某一些文章中的词拥有较大的权重,而那些频繁出现在很多文章中的词(毫无信息上的帮助)拥有较小的权重。\(idf_{t}\)可以表示为: \(idf_{t} = \frac{N}{df_{t}}\) 其中,N为语料库中文章的总数,\(df_{t}\)为词t所出现的文章的总数。词t出现的文章越少,它越具备区分能力,\(idf_{t}\)越大。同样为了压缩一下IDF值的大小,对其取对数如下: \(idf_{t} = log_{10}(\frac{N}{df_{t}+1})\)
\(idf_{t}的分母中加1是为了避免分母为0\)
最后,\(TF-IDF = tf_{t,d} \times idf_{t}\)
Python代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39import math
def loadDataSet():
dataset = [
['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid'],
] #随便的一组示例数据
return dataset
def tf_idf(t, d, data_list):
#词t 文档d
#tf
count_t = 0
for word in data_list[d]:
if word == t:
count_t += 1
tf = count_t / len(data_list[d])
#idf
N = len(data_list)
df = 0
for i in range(len(data_list)):
if t in data_list[i]:
df += 1
idf = math.log(N/(df+1),10)
# print(idf)
return tf*idf
if __name__ == '__main__':
data_list = loadDataSet() #加载数据
tf_idf_value= list()
for d in range(len(data_list)): #文章的序号
d_word = dict() #记录d中所有词的tf-idf
#文章d中词t的tf-idf
for i in range(len(data_list[d])):
t = data_list[d][i]
d_word[t] = tf_idf(t, d, data_list)
tf_idf_value.append(d_word)
print(tf_idf_value)