Why Transformer?
Transformer 是Google Brain在2017年的《Attention Is All You Need》中提出的。
Transformer针对RNN的弱点进行重新设计，解决了RNN效率问题和传递中的缺陷等。RNN对sequence（序列）进行串行的处理，Transformer对sequence进行并行的处理。
What is Transformer?
The Transformer - model architecture: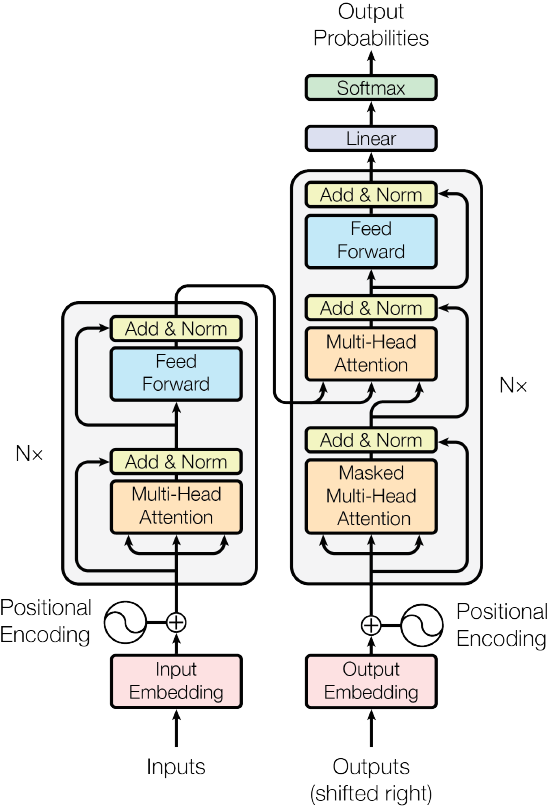 
它是基于Encoder-Decoder结构的模型，在Encoder和Decoder中各有N个不同的Transformer block。
Positional Encoding
在Transformer中没有RNN的迭代操作（前一输出成为当下的输入），sequence中所有的word都被同等对待，所以word之间没有了先后关系，因此，Transformer架构中提出了Positional Encoding方案，给每个输入的词向量叠加一个固定的位置向量来区分位置关系。
位置编码需要满足以下准则：参考 * 每个位置的编码是唯一的。 * 相邻位置的编码值的差都是相同的。 * 编码的方法要能轻松泛化到更长的句子。 * 编码的方式必须是确定的。
在Transformer中的编码方法：Position Embedding给每个位置编码为一个d维向量\(\vec{p_t}\)，t表示句子中位置： \[ \vec{p_t} = \begin{bmatrix} \sin (\omega_1 \cdot t) \\ \cos (\omega_1 \cdot t) \\ \sin (\omega_2 \cdot t) \\ \cos (\omega_2 \cdot t) \\ \cdots \\ \sin (\omega_d/2 \cdot t) \\ \cos (\omega_d/2 \cdot t) \\ \end{bmatrix} \] 其中\(\omega_k = \frac{1}{10000^{2k/d}}\),k为1到d/2区间的整数。
为什么结合正余弦函数就能表示不同的位置？
参考 首先，我们可以通过一个4维的二进制向量来表示不同的位置值: 
通过观察可以看出最低位的变化是最快的，而最高位的变化十分缓慢。这种方式在浮点数的世界看来十分奢侈，因为位置全都是整数。因此用正弦函数和余弦函数来模拟这种变化：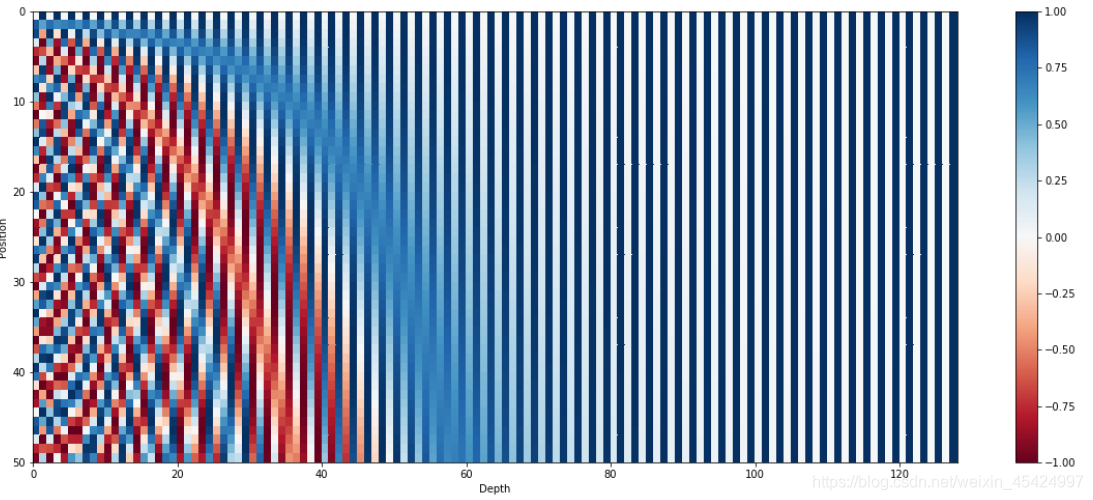 
上图是为利用128维的向量对位置进行编码，总共用50个128维向量编码了50个位置(编码了长度为50的句子)。同样，最低位变化地十分快，而最高位的编码几乎没变。
另外，这种编码方式能够让模型轻松学到不同位置之间的相关性，因为对于任意一偏移(offset)k,\(\vec{p_{t+k}}\)可以被表示为\(\vec{p_t}\)的线性函数。依据上面的\(\vec{p_t}\)公式和三角函数的变换公式:\(\sin {a+b} = \sin a \cdot \cos b + \cos a \cdot \sin b\)、\(\cos {a+b} = \cos a \cdot \cos b - \sin a \cdot \sin b\)可以得出。
关于为什么Word Embedding和Position Embedding相加 ## Encoder部分
Transformer是一个N进N出的结构，接收一整个句子所有词作为输入，然后为句子中的每个词都做出一个输出。与RNN不同的是，Transformer能够同时处理句子中的所有词，RNN一次只能处理一个词。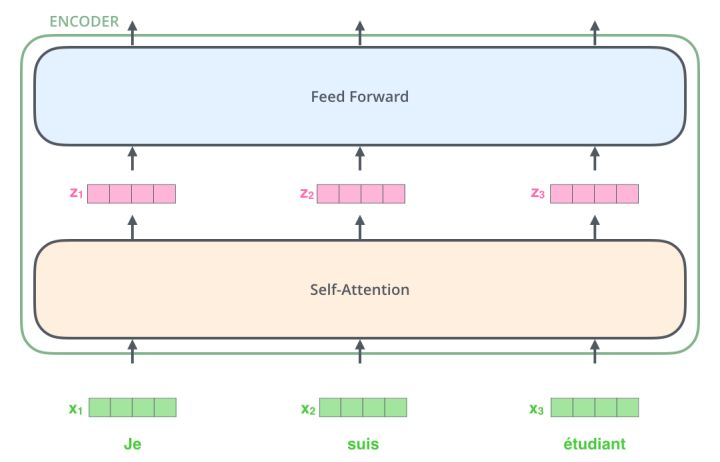 
（一个句子中所有的词同时进入到Encoder进行处理。） 每个Transformer block都有两个最重要的子层，分别是Self-Attention层与Feed Forward层。
- Self-Attention层
对比RNN:
Attenrion就是为了关注到数据中有价值的信息，提取数据中不同的关注点。比如下面这个句子中"it"的是指什么呢？ "The animal didn't cross the street because it was too tired" self-attention将"it"与"animal"联系起来。模型在处理句子中每个词的时候，self-attention允许输入序列中的词互相查看来找到对词更好编码的线索。如下图，在编码"it"时，部分注意力机制关注在"The animal"，并以一定程度将它的表示加入到"it"的编码中。
- 解析self-attention。(计算过程，图片来自李宏毅老师的视频(b站),还有Jay Alammar大佬的博客)
- 对每个词向量生成q,k,v
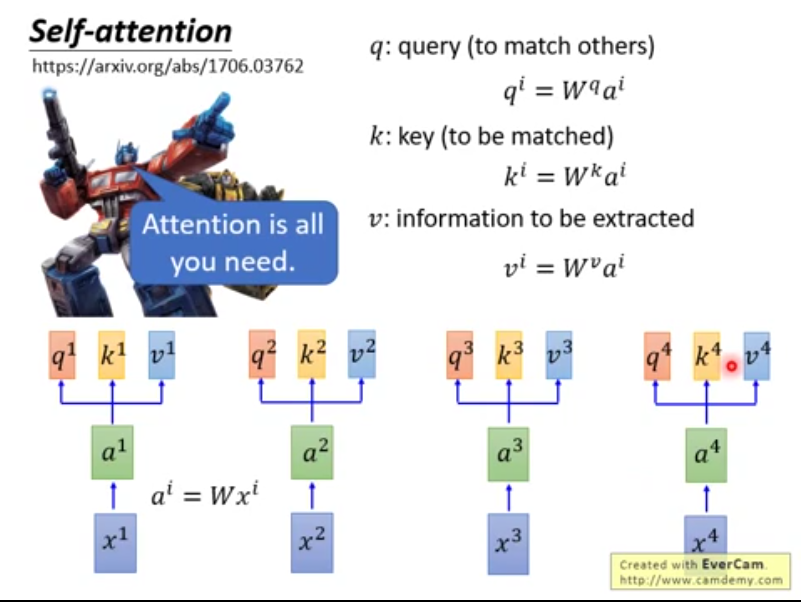
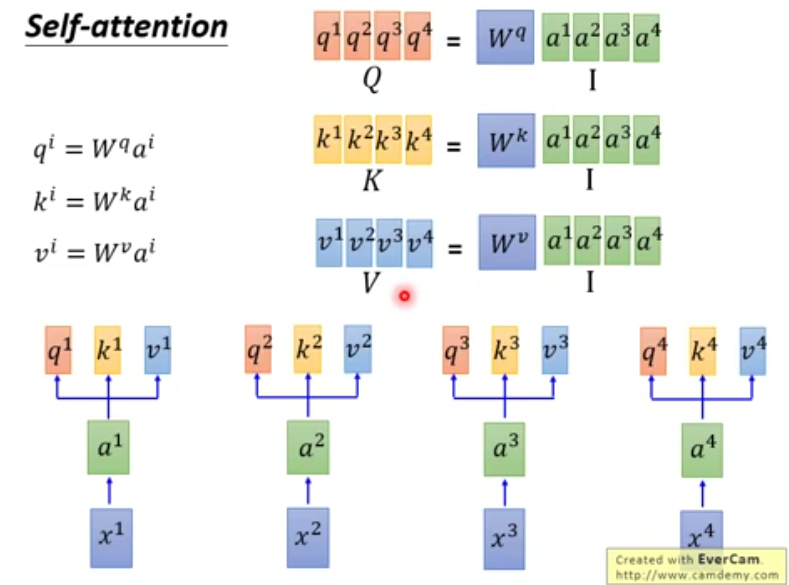
- 每个query q对每个key k做attention(计算得分)
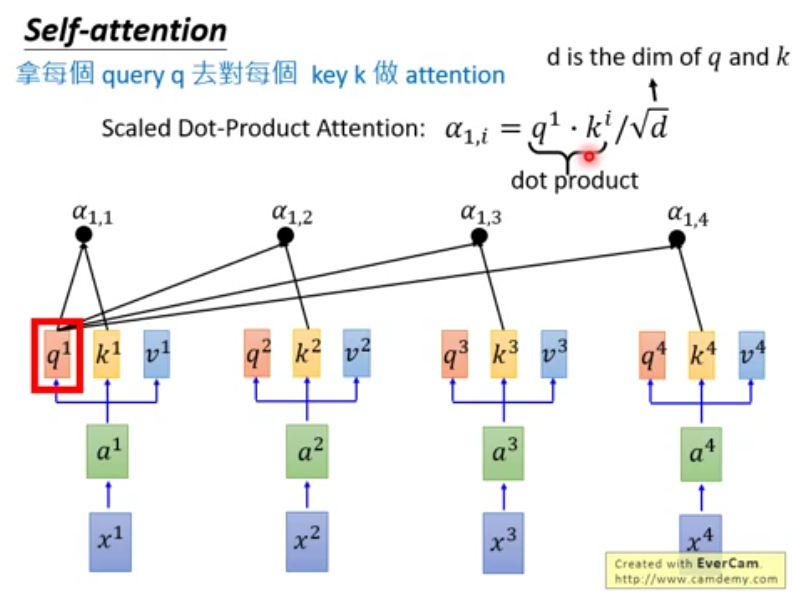scaled是为了让attention的得分值不随着向量维度的增大而增大,防止点积过大让相应数值softmax函数的梯度变得很小很小，使得下面的softmax之后的结果更加稳定。 所有的q和k相乘即为如下的矩阵乘法：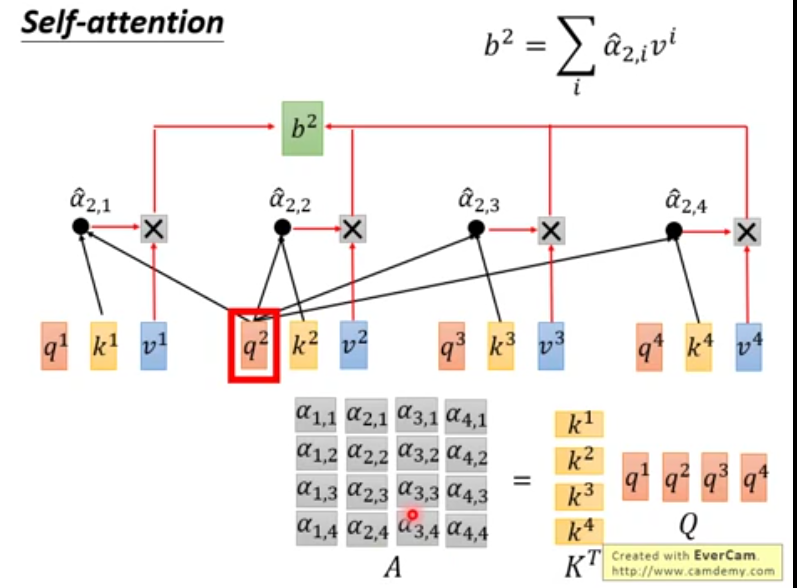 
- 做完attention后进行softmax
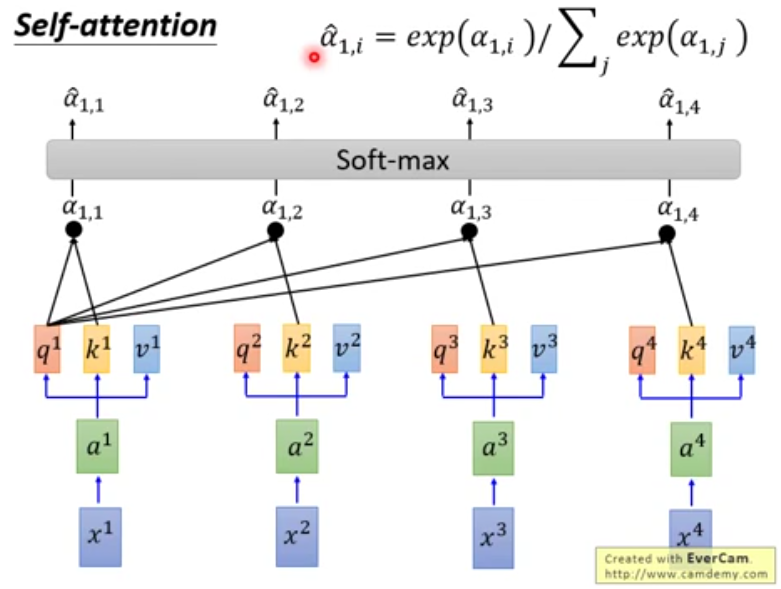通过attention得到的得分值再应用softmax变为比例(权重)知道每个词对自己的影响程度。 - 用注意力向量的权重（上一步softmax的结果）给V进行加权
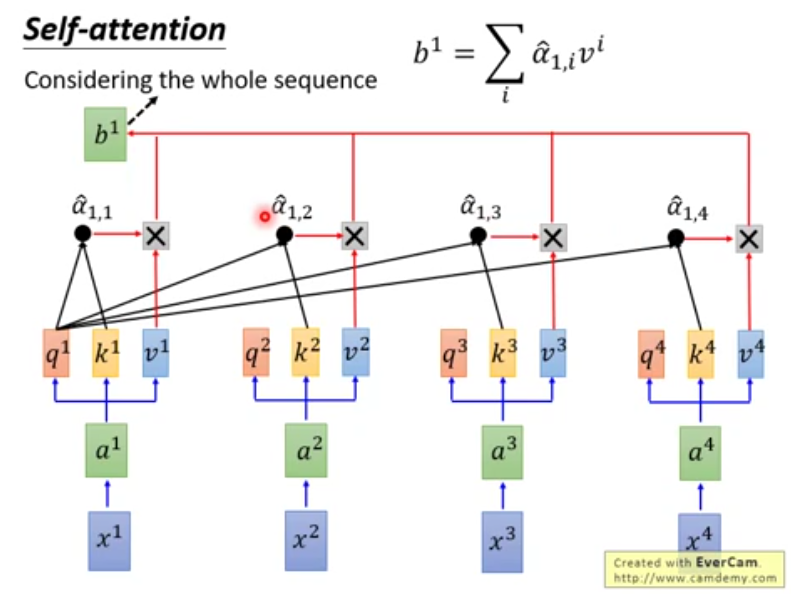b2,b3,b4同样计算，因为互不干扰，所以可以（同时）并行计算也就是如下的矩阵运算。 
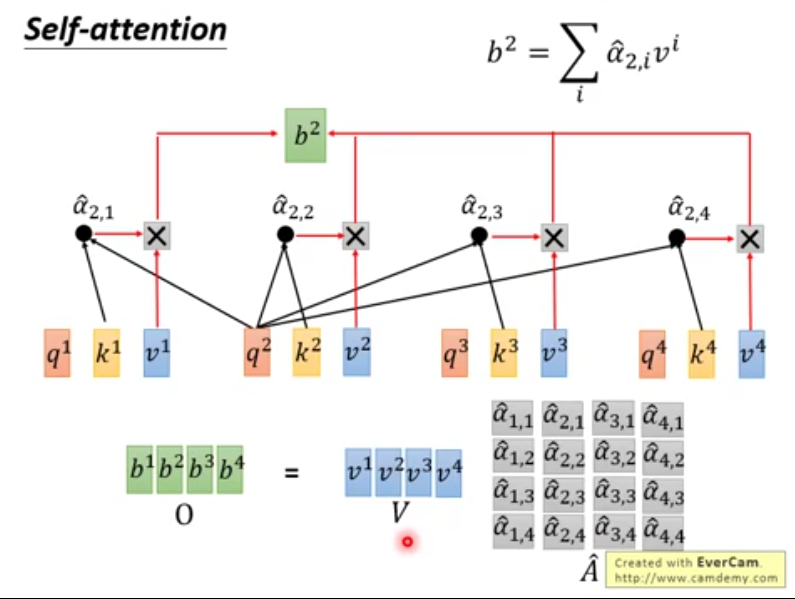总的来说,self-attention的矩阵运算如下： 
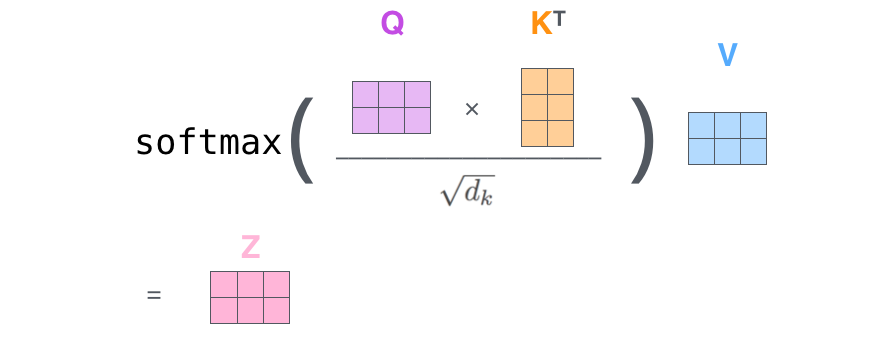(下图中中O矩阵也就是上图中的Z矩阵) 
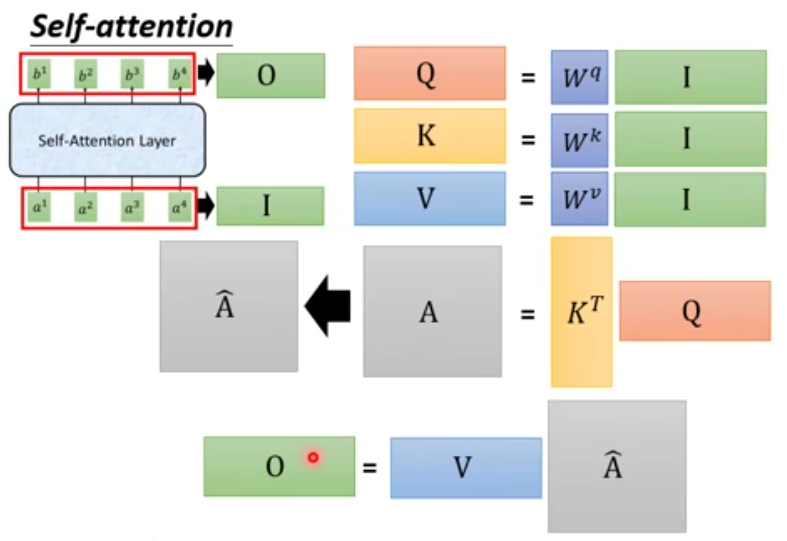Self-attention就是一堆矩阵乘法(加速)。由此看来，不同的输入序列中相同词可以学到不同的含义。
- Multi-head self-attention 将原来的q,k,v做分裂，下面为2个head的例子，head数为超参数可以调。
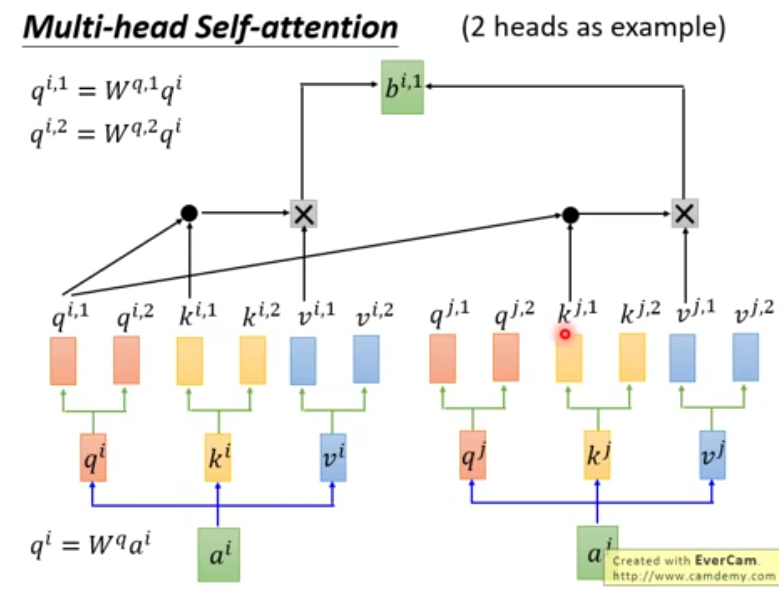之所以要把原来的q,k,v再细分是为了可以做到更多的事情，多了q就可以设置它去关注不同的内容，比如只关注local或者关注较远位置的信息或者只关注前面的信息等等。 通过不同的head得到多个特征表达，将得到的不同的特征表达拼接在一起然后通过一层全连接层(线性变换)来降维(降维到词向量的编码长度)。 
- Feedforward层：两层线性映射（输入乘上它的权重系数---就是线性映射）并用激活函数激活。
Decoder
- 根据当前的Encoder学到的Attention和一个一个输入的词进行预测。
- Decoder端不仅要根据自己要预测的词所得到的Attention（主要用Q query）还要依据Encoder端的Attention（K key,V value）进行预测。
- Decoder和Encoder过程是类似的。 区别在于：加入了Masked multi-head attention。加入mask是为了预测后一个word的时候没有提前看到答案。