Space and time

When we refer to the efficiency of a program, we aren't just thinking about its speed—we're considering both the time it will take to run the program and the amount of space the program will require in the computer's memory. Often there will be a trade-off between the two, where you can design a program that runs faster by selecting a data structure that takes up more space—or vice versa.

Algorithms

An algorithm is essentially a series of steps for solving a problem. Usually, an algorithm takes some kind of input (such as an unsorted list) and then produces the desired output (such as a sorted list).

For any given problem, there are usually many different algorithms that will get you to exactly the same end result. But some will be much more efficient than others. To be an effective problem solver, you'll need to develop the ability to look at a problem and identify different algorithms that could be used—and then contrast those algorithms to consider which will be more or less efficient.

But computers are so fast!

Sometimes it seems like computers run programs so quickly that efficiency shouldn't really matter. And in some cases, this is true—one version of a program may take 10 times longer than another, but they both still run so quickly that it has no real impact.

But in other cases, a small difference in how your code is written—or a tiny change in the type of data structure you use—can mean the difference between a program that runs in a fraction of a millisecond and a program that takes hours (or even years!) to run.

In thinking about the efficiency of a program, which is more important: The time the program will take to run, or the amount of space the program will require?

○ The time complexity of the problem is more important ○ The space complexity of the problem is more important ○ It really depends on the problem

SOLUTION: It really depends on the problem

Quantifying efficiency

It's fine to say "this algorithm is more efficient than that algorithm", but can we be more specific than that? Can we quantify things and say how much more efficient the algorithm is?

Let's look at a simple example, so that we have something specific to consider.

Here is a short (and rather silly) function written in Python: 

1
2
3
4
def some_function(n):
for i in range(2):
    n += 100
return n
What does it do? ○ Adds 2 to the given input. ○ Adds 200 to the given input. ○ Adds 100 to the given input. SOLUTION: Adds 200 to the given input.

Now how about this one? 

1
2
3
4
def other_function(n):
for i in range(100):
    n += 2
return n
What does it do? ○ Adds 2 to the given input. ○ Adds 200 to the given input. ○ Adds 100 to the given input. SOLUTION: Adds 200 to the given input.

So these functions have exactly the same end result. But can you guess which one is more efficient?

Here they are next to each other for comparison: 

1
2
3
4
5
6
7
8
def some_function(n):
for i in range(2):
    n += 100
return n
def other_function(n):
for i in range(100):
    n += 2
return n
○ some_function is more efficient ○ other_function is more efficient ○ They have exactly the same efficiency SOLUTION: some_function is more efficient

Although the two functions have the exact same end result, one of them iterates many times to get to that result, while the other iterates only a couple of times.

This was admittedly a rather impractical example (you could skip the for loop altogether and just add 200 to the input), but it nevertheless demonstrates one way in which efficiency can come up.

Counting lines

With the above examples, what we basically did was count the number of lines of code that were executed. Let's look again at the first function: 

1
2
3
4
def some_function(n):
for i in range(2):
    n += 100
return n
There are four lines in total, but the line inside the for loop will get run twice. So running this code will involve running 5 lines.

Now let's look at the second example: 

1
2
3
4
def other_function(n):
for i in range(100):
    n += 2
return n
In this case, the code inside the loop runs 100 times. So running this code will involve running 103 lines!

Counting lines of code is not a perfect way to quantify efficiency, and we'll see that there's a lot more to it as we go through the program. But in this case, it's an easy way for us to approximate the difference in efficiency between the two solutions. We can see that if Python has to perform an addition operation 100 times, this will certainly take longer than if it only has to perform an addition operation twice!

Input size and efficiency

Here's one of our functions from the last page: 

1
2
3
4
def some_function(n):
for i in range(2):
    n += 100
return n
Suppose we call this function and give it the value 1, like this: 
1
some_function(1)
And then we call it again, but give it the input 1000: 
1
some_function(1000)
Will this change the number of lines of code that get run? ○ Yes — some_function(1000) will involve running more lines of code. ○ Yes — some_function(1) will involve running more lines of code. ○ No — the same number of lines will run in both cases. SOLUTION: No — the same number of lines will run in both cases.

Now, here's a new function: 

1
2
3
def say_hello(n):
for i in range(n):
    print("Hello!")
Suppose we call it like this: 
1
say_hello(3)
And then we call it like this: 
1
say_hello(1000)
Will this change the number of lines of code that get run? ○ Yes — say_hello(3) will involve running more lines of code. ○ Yes — say_hello(1000) will involve running more lines of code. ○ No — the same number of lines will run in both cases. SOLUTION: Yes — say_hello(1000) will involve running more lines of code.

This highlights a key idea:As the input to an algorithm increases, the time required to run the algorithm may also increase.

Notice that we said may increase. As we saw with the above examples, input size sometimes affects the run-time of the program and sometimes doesn't—it depends on the program.

The rate of increase

QUIZ QUESTION:: Let's look again at this function from above: 

1
2
3
def say_hello(n):
for i in range(n):
    print("Hello!")
Here's a question about the function (from the above exercise). When we increase the size of the input n by 1, how many more lines of code get run? ○ When n goes up by 1, the number of lines run also goes up by 1. ○ When n goes up by 1, the number of lines run goes up by 2. ○ When n goes up by 1, the number of lines run goes up by 4. SOLUTION: When n goes up by 1, the number of lines run also goes up by 1.

So here's one thing that we know about this function: As the input increases, the number of lines executed also increases.

But we can go further than that! We can also say that as the input increases, the number of lines executed increases by a proportional amount. Increasing the input by 1 will cause 1 more line to get run. Increasing the input by 10 will cause 10 more lines to get run. Any change in the input is tied to a consistent, proportional change in the number of lines executed. This type of relationship is called a linear relationship, and we can see why if we graph it: 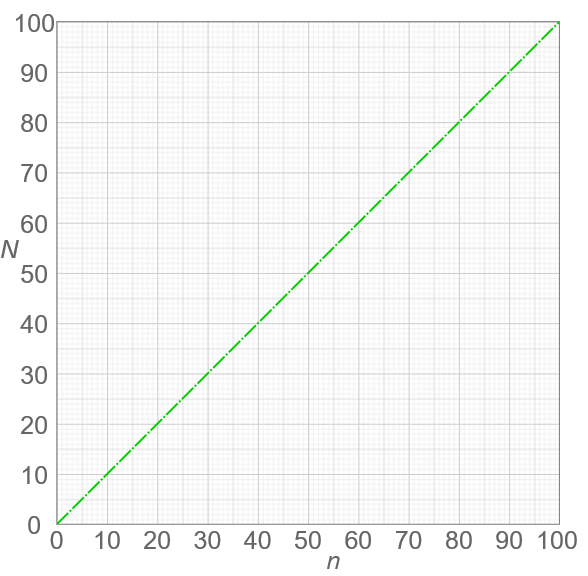Derivative of "Comparison of computational complexity" by Cmglee. Used under CC BY-SA 4.0.

The horizontal axis, n, represents the size of the input (in this case, the number of times we want to print "Hello!"). The vertical axis, N, represents the number of operations that will be performed. In this case, we're thinking of an "operation" as a single line of Python code (which is not the most accurate, but it will do for now).

We can see that if we give the function a larger input, this will result in more operations. And we can see the rate at which this increase happens—the rate of increase is linear. Another way of saying this is that the number of operations increases at a constant rate. If that doesn't quite seem clear yet, it may help to contrast it with an alternative possibility—a function where the operations increase at a rate that is not constant.

QUIZ QUESTION:: Now here's a slightly modified version of the say_hello function: 

1
2
3
4
def say_hello(n):
for i in range(n):
    for i in range(n):
        print("Hello!")
Notice that it has a nested loop (a for loop inside another for loop!).

Looking at the say_hello function from the above exercise, what can we say about the relationship between the input, n, and the number of times the function will print "Hello!"? ○ The function will always print "Hello!" the same number of times (changing n doesn't make a difference). ○ The function will print "Hello!" exactly n times (so say_hello(2) will print "Hello!" twice). ○ The function will print "Hello!" exactly n-squared times (so say_hello(2) will print "Hello!" 22 or four times). SOLUTION: The function will print "Hello!" exactly n-squared times (so say_hello(2) will print "Hello!" 22 or four times).

Notice that when the input goes up by a certain amount, the number of operations goes up by the square of that amount. If the input is 2, the number of operations is 2^2 or 4. If the input is 3, the number of operations is 3^2 or 9.

To state this in general terms, if we have an input, nnn, then the number of operations will be n^2. This is what we would call a quadratic rate of increase.

Let's compare that with the linear rate of increase. In that case, when the input is n, the number of operations is also n. Let's graph both of these rates so we can see them together: 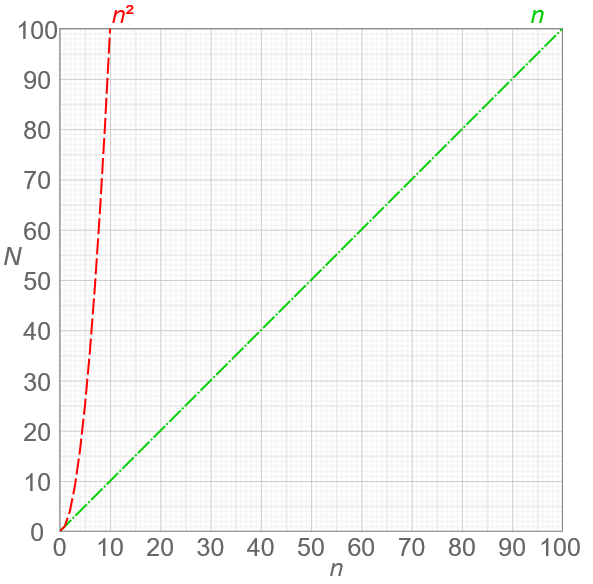Derivative of "Comparison of computational complexity" by Cmglee. Used under CC BY-SA 4.0.

Our code with the nested for loop exhibits the quadratic n^2 relationship on the left. Notice that this results in a much faster rate of increase. As we ask our code to print larger and larger numbers of "Hellos!", the number of operations the computer has to perform shoots up very quickly—much more quickly than our other function, which shows a linear increase.

This brings us to a second key point. We can add it to what we said earlier:As the input to an algorithm increases, the time required to run the algorithm may also increase—and different algorithms may increase at different rates.

Notice that if n is very small, it doesn't really matter which function we use—but as we put in larger values for n, the function with the nested loop will quickly become far less efficient. We've looked here only at a couple of different rates—linear and quadratic. But there are many other possibilities. Here we'll show some of the common types of rates that come up when designing algorithms: 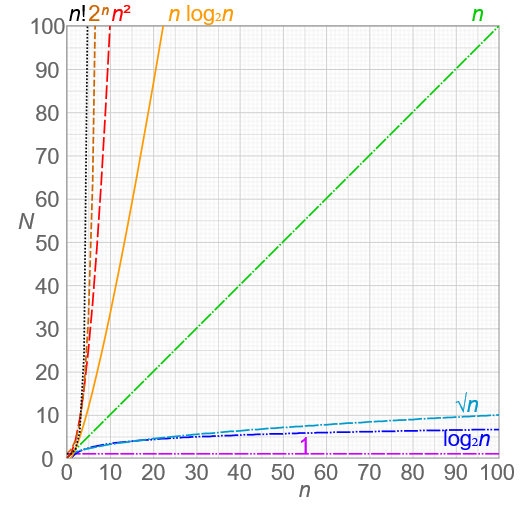"Comparison of computational complexity" by Cmglee. Used under CC BY-SA 4.0.

We'll look at some of these other orders as we go through the class. But for now, notice how dramatic a difference there is here between them! Hopefully you can now see that this idea of the order or rate of increase in the run-time of an algorithm is an essential concept when designing algorithms.

Order

We should note that when people refer to the rate of increase of an algorithm, they will sometimes instead use the term order. Or to put that another way:The rate of increase of an algorithm is also referred to as the order of the algorithm.

For example, instead of saying "this relationship has a linear rate of increase", we could instead say, "the order of this relationship is linear".

On the next page, we'll introduce something called Big O Notation, and you'll see that the "O" in the name refers to the order of the rate of increase.

Big O Notation

When describing the efficiency of an algorithm, we could say something like "the run-time of the algorithm increases linearly with the input size". This can get wordy and it also lacks precision. So as an alternative, mathematicians developed a form of notation called big O notation.

The "O" in the name refers to the order of the function or algorithm in question. And that makes sense, because big O notation is used to describe the order—or rate of increase—in the run-time of an algorithm, in terms of the input size (n).

Udacity数据结构与算法