递归

1 什么是递归？

递归的思想就是函数调用函数本身。像下面的伪码中所示： 

1
2
3
4
5
6
function recursive(input):
	if input <= 0
		return input
	else
		output = recursive(input - 1)
		return output
递归函数：

  • 1.递归函数需要在函数内部的某处调用自己。
  • 2.递归函数需要一个base case(基础情况)，也就是递归终止的条件。

在某些方面看来递归就像一个while循环，一直循环某些代码直到满足退出循环的条件。

1
2
3
4
5
while(exit condition):
	code
	code 
	code
	code

如果没有写好base case，也就是递归终止的条件，程序就会陷入到无限的循环递归中。

注意思考递归输入的数据范围，防止有些输入不在递归终止的条件中。比如上述递归代码中，if input <= 0变为if input == 0，那么输入为负数的话永远到不了递归结束条件(input==0)

  • 3.递归函数需要改变。递归的输入要有改变，否则就会陷入到无限的递归中即每次都递归同样的输入是不可能抵达递归终止条件的。

2 递归的时间复杂度

考虑递归函数的时间复杂度，需要根据具体的递归方程或者说递归方式来计算。

示例1

以一个例子来看。给定一个正整数n，print_integers函数递归打印n到1的数。 

1
2
3
4
5
6
def print_integers(n):
    if n <= 0:
        return
    else:
        print(n)
        print_integers(n - 1)
调用print_integers函数： 
1
print_integers(5)
print_integers(5)的调用如下图所示，下图中调用栈的栈顶在最下面,也就是n为0的帧(frame)是调用栈的栈顶。

令 print_integers(n)的执行时间为\(T(n)\)，执行函数内部简单操作的时间为常数\(k\)。那么：

\[T(n) = T(n - 1) + k\]

其中\(T(n - 1)\)代表执行print_integers(n - 1)函数的时间.

同样的，\(T(n - 1)\)可以表示为：

\[T(n - 1) = T(n - 2) + k\]

根据上述规律可以写出：

  1. \(T(n)\ \ \ \ \ \ \ = T(n - 1) + k\)
  2. \(T(n - 1) = T(n - 2) + k\)
  3. \(T(n - 2) = T(n - 3) + k\)
  4. \(T(n - 3) = T(n - 4) + k\) .
    .
    .
    .
    .
    .
  5. \(T(2) = T(1) + k\)
  6. \(T(1) = T(0) + k\)
  7. \(T(0) = k1\)

当n = 0时只需要执行最简单的情况(base case), 时间为常数\(k1\).

如果将上面的方程式左边相加同时右边相加，最后可以得到：

\[T(n) = nk + k1\]

当我们计算时间复杂度时，通常会忽略式子中加上的常数，因为对于输入规模在\(10^5\)时这些加上的常数可以忽略不计。所以上述可以简化为：

\[T(n) = nk \]

可以看到print_integers(n)函数的时间复杂度是n的线性函数，所以时间复杂度为： \(O(n)\)。

示例2

二分查找可以用递归的方式来实现(它也可以用迭代的方式来实现)。分析递归实现的二分查找的时间复杂度。

二分查找的递归实现如下所示： 

1
2
3
4
5
6
7
8
9
10
11
12
13
def binary_search(arr, target):
    return binary_search_func(arr, 0, len(arr)-1, target)

def binary_search_func(arr, start_index, end_index, target):
    if start_index > end_index:
        return -1
    mid_index = (start_index + end_index) // 2
    if arr[mid_index] == target:
        return min_index
    elif arr[mid_index] < target:
        return binary_search_func(arr, mid_index+1, end_index, target)
    else:
        return binary_search_func(arr, start_index, mid_index-1, target)
binary_search()函数直接调用了binary_search_func()，所以时间复杂度完全依赖binary_search_func()的时间复杂度.

binary_search_func()的时间复杂度是输入规模n的函数，\(T(n)\).

binary_search_func()中base case和其他赋值与比较的操作与输入规模无关，执行时间为常数k，除了这些常数时间的操作外，函数要么调用左半边输入(数组)要么调用右半边输入(数组)，通过这样的操作，输入规模缩减为了\(n/2\)，所以时间复杂度变为\(T(n/2)\)，也就是：

\[T(n) = T(n/2) + k\]

同样地，调用一半输入数据的函数执行时间为：

\[T(n/2) = T(n/4) + k\]

类似有： 1. \(T(n)\ \ \ = T(n/2) + k\) 2. \(T(n/2) = T(n/4) + k\) 3. \(T(n/4) = T(n/8) + k\) 4. \(T(n/8) = T(n/16) + k\) .
.
.
.
.
.
5. \(T(4) = T(2) + k\) 6. \(T(2) = T(1) + k\) 7. \(T(1) = T(0) + k1\) \(^{(1)}\)
8. \(T(0) = k1\)

\(^{(1)}\) 如果只有一个元素，那么接下来的就是0个元素。

所以方程式左边相加同时右边相加得到：

\[T(n) = log(n) * k + k1\]

忽略加的常数：

\[T(n) = log(n) * k \]

所以，递归实现的二分查找的时间复杂度为O(log(n))

3 递归的应用

递归应用在特定问题的解决方案依靠相同问题的更小实例的解决这种场景下。

例如：计算\(\mathtt{2^5}\). 我们需要\(2 * 2 * 2 * 2 * 2\). 已知\(2^5 = 2 * 2^4\).如果我们知道\(2^4\), 就能轻易地计算出\(2^5\).因为(\(2^n\))的求解依赖同样问题的更小实例(\(2^{n-1}\))，所以使用递归来解决.所以，递归的方案就是对于所有大于0的n计算\(2 * 2^{n-1}\)，如果n为0则返回1.(忽略负数)

利用递归计算\(2^5\)的步骤即为：

\(2^5 = 2 \* 2^4\)

\(2^5 = 2 \* 2 \* 2^3\)

\(2^5 = 2 \* 2 \* 2 \* 2^2\)

\(2^5 = 2 \* 2 \* 2 \* 2 \* 2^1\)

\(2^5 = 2 \* 2 \* 2 \* 2 \* 2 \* 2^0\)

\(2^5 = 2 \* 2 \* 2 \* 2 \* 2 \* 1\)

python实现求\(2^n\)： 

1
2
3
4
5
def power_of_2(n):
    if n == 0:
        return 1
    else:
        return 2*power_of_2(n-1)
练习 实现sum_integers(n)函数，利用递归计算从1到n的整数和。 
1
2
3
4
5
def sum_integers(n)：
	if n == 1:
		return 1
	else:
		return n + sum_integers(n-1)
————

3.1 阶乘函数

阶乘函数(factorial function)用于计算给定数n和其余所有从n到1的的乘积。

例如n=4: \(4\*3\*2\*1 = 24\) 也就是:\(4! = 4\*3\*2\*1 = 24\)

一般地，对于任意输入\(n\): \(n! = n \* (n-1) \* (n-2) ... 1\)

仔细观看可以看出上式可以写成下面的形式： \(n! = n\*(n-1)!\) 利用递归可以轻松实现。

\(0! = 1\) 

1
2
3
4
5
def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)
测试用例： 
1
2
3
4
print(factorial(4))
print ("Pass" if (1 == factorial(0)) else "Fail")
print ("Pass" if  (1 == factorial(1)) else "Fail")
print ("Pass" if  (120 == factorial(5)) else "Fail")
—————

3.2 反转字符串

利用递归的方式实现字符串的反转。

python有内置的reverse函数实现字符串的反转，在这里需要自己用递归来实现。

1
2
3
4
5
6
7
8
9
10
11
12
def reverse_string(input_string):
    if len(input_string) == 1:
        return input_string
    elif len(input_string) == 0:
        return ''
    else:
        tail = input_string[0] 
        head = input_string[len(input_string)-1]
        if len(input_string) == 2:
            return head+tail
        else:
            return head+reverse_string(input_string[1:len(input_string)-1])+tail

测试用例： 

1
2
3
4
print ("Pass" if  ("" == reverse_string("")) else "Fail")
print ("Pass" if  ("cba" == reverse_string("abc")) else "Fail")
print(reverse_string('abc'))
print(reverse_string('abcdefg'))
————

3.3 逆序栈

给定一个栈，请你逆序这个栈，不能申请额外的数据结构，只能使用递归函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def get_bottom(stack):
    current = stack.pop()
    if len(stack) == 0:
        return current
    bottom = get_bottom(stack)
    stack.append(current)
    return bottom
def reverse_stack(stack):
    if len(stack) == 0:
        return
    bottom = get_bottom(stack)
    reverse_stack(stack)
    stack.append(bottom)
    return stack

stack = [90, 34, 3, 4]
print(reverse_stack(stack))

3.4 回文串(Palindrome)

回文串是指正序和逆序相同的字符串。

例如： * "madam" is a palindrome * "abba" is a palindrome * "cat" is not * "a" is a trivial case of a palindrome

利用递归的方式，实现is_palindrome函数，输入为一个字符串，判断该字符串是否为回文串。 

1
2
3
4
5
def is_palindrome(input):
    if len(input) == 0 or len(input) == 1:
        return True
    else:
        return input[0] == input[len(input)-1] and is_palindrome(input[1:len(input)-1])
测试用例： 
1
2
3
4
5
print ("Pass" if  (is_palindrome("")) else "Fail")
print ("Pass" if  (is_palindrome("a")) else "Fail")
print ("Pass" if  (is_palindrome("madam")) else "Fail")
print ("Pass" if  (is_palindrome("abba")) else "Fail")
print ("Pass" if not (is_palindrome("Udacity")) else "Fail")
### 3.5 九键组合

九键(keypad)就是手机上字母分布在数字2到9上的键盘。通过点不同的数字形成不同的字母组合，例如按下23，可能的字母组合就有：da, db, dc, ea, eb, ec, fa, fb, fc

给定一个整数num，找出其中数字顺序代表的所有可能的字符序列(字符串)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def get_characters(num):
    if num == 2:
        return "abc"
    elif num == 3:
        return "def"
    elif num == 4:
        return "ghi"
    elif num == 5:
        return "jkl"
    elif num == 6:
        return "mno"
    elif num == 7:
        return "pqrs"
    elif num == 8:
        return "tuv"
    elif num == 9:
        return "wxyz"
    else:
        return ""

def keypad(num):
    if num == 0:
        return ['']
    elif num < 10:
          return list(get_characters(num))
    else:
        num = str(num)
        output = []
        string = ''

        tmp = list(get_characters(int(num[0])))
        sub_keypad = keypad(int(num[1:]))
        for head in tmp:
            for s in sub_keypad:
                output.append(head + s)
        return output
测试函数： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def test_keypad(input, expected_output):
    if sorted(keypad(input)) == expected_output:
        print("Yay. We got it right.")
    else:
        print("Oops! That was incorrect.")

input = 0
expected_output = [""]
test_keypad(input, expected_output)

# Example case
input = 23
expected_output = sorted(["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"])
test_keypad(input, expected_output)

input = 8
expected_output = sorted(["t", "u", "v"])
test_keypad(input, expected_output)

input = 354
expected_output = sorted(["djg", "ejg", "fjg", "dkg", "ekg", "fkg", "dlg", "elg", "flg", "djh", "ejh", "fjh", "dkh", "ekh", "fkh", "dlh", "elh", "flh", "dji", "eji", "fji", "dki", "eki", "fki", "dli", "eli", "fli"])
test_keypad(input, expected_output)
### 3.6 深度反转

实现深度反转函数deep_reverse,输入为列表，输出深度反转后的列表即如果列表元素依旧是列表的话也需要将其反转。

函数不能改变初始输入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def deep_reverse(arr):
    if len(arr) == 0:
        return arr
    if len(arr) == 1:
        if type(arr[0]) == list:
            return [deep_reverse(arr[0])]
        else:
            return arr
    else:
        head = arr[-1]
        tail = arr[0]
        if type(head) == list:
            head = deep_reverse(head)
        if type(tail) == list:
            tail = deep_reverse(tail)
        result = [head] + deep_reverse(arr[1:len(arr)-1]) + [tail]
        return result

测试用例： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def test_function(test_case):
    arr = test_case[0]
    solution = test_case[1]
    
    output = deep_reverse(arr)
    if output == solution:
        print("Pass")
    else:
        print("False")

arr = [1, 2, 3, 4, 5]
solution = [5, 4, 3, 2, 1]
test_case = [arr, solution]
test_function(test_case)

arr = [1, 2, [3, 4, 5], 4, 5]
solution = [5, 4, [5, 4, 3], 2, 1]
test_case = [arr, solution]
test_function(test_case)

arr = [1, [2, 3, [4, [5, 6]]]]
solution = [[[[6, 5], 4], 3, 2], 1]
test_case = [arr, solution]
test_function(test_case)

arr =  [1, [2,3], 4, [5,6]]
solution = [ [6,5], 4, [3, 2], 1]
test_case = [arr, solution]
test_function(test_case)
### 3.7 汉诺塔(tower of Hanoi)

汉诺塔问题就是将A针(source)上所有N个盘子移动至C针(destination),一次只能移动一个，小盘子必须在大盘子上面,问：总共需要移动多少次？

对于B针(auxiliary)，可以将之看成一个中转站。

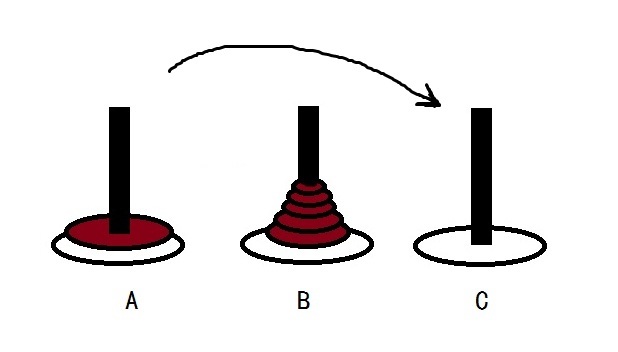
实现tower_of_Hanoi函数，求解汉诺塔问题。输出格式为：

S A S D A D
其中， S = source(A针), D = destination(C针), A = auxiliary(B针)

1
2
3
4
5
6
7
8
9
10
11
12
def tower_of_Hanoi(num_disks):
    return tower_of_Hanoi_func(num_disks, 'S', 'A', 'D')
def tower_of_Hanoi_func(num_disks, source, auxiliary, destination):
    if num_disks == 0:
        return
    elif num_disks == 1:
        print(source, destination)
        return
    else:
        tower_of_Hanoi_func(num_disks-1, source, destination, auxiliary)
        print(source, destination )
        tower_of_Hanoi_func(num_disks-1, auxiliary, source, destination)

测试用例： 

1
tower_of_Hanoi(2)
* num_disks = 2

    S A
    S D
    A D
1
tower_of_Hanoi(3)

  • num_disks = 3

      S D
  S A
  D A
  S D
  A S
  A D
  S D
    1
    tower_of_Hanoi(4)

  • num_disks = 4

      S A
  S D
  A D
  S A
  D S
  D A
  S A
  S D
  A D
  A S
  D S
  A D
  S A
  S D
  A D

3.8 编码

规定1和a对应，2和b对应，3和c对应，以此类推，直到26和z对应。给定一个只有数字字符组成的字符串number，返回有多少种转化结果codes_possible。具体可以看下面的例子。

Example 1

  • number = '123'
  • codes_possible = ["aw", "abc", "lc"]

解释：

  • 1 / 23 = "aw"
  • 1 / 2 / 3 = "abc"
  • 12 / 3 = "lc"

Example 2

  • number = '145'
  • codes_possible = ["ade", "ne"]

思路： 假设 0 到 (i-1) 位置的数字已经确定好转化的结果，那么对于 i 位置，根据它位置的数值，分类进行决策： - 如果 i 位置的数为 0 ，那么当前可以转化的情况是空，也就是没有（因为前面的已经确定好转化了，而0也没办法和下面的数值结合）； - 如果 i 位置的数为 1，这时进行两种决策，第一种选择自己单独转化，第二种选择自己和下一个数字共同进行转化； - 如果 i 位置的数为 2，这时进行两种决策，第一种选择自己单独转化，第二种选择自己和下一个数字共同进行转化(这里要判断结合的数值是否小于26)； - 如果 i 位置的数为 3-9，这时只有一种决策，也就是自己单独转化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def all_codes(number, i, code, result):
    if i == len(number) - 1:
        code.append(chr(int(number[i])+96))
        result.append(''.join(code))
        return
    if i > len(number) - 1:
        result.append(''.join(code))
        return
    if number[i] == '0':
        # all_codes(number, i+1, code[:], result)
        return
    elif number[i] == '1':
        code.append(chr(int(number[i])+96))
        all_codes(number, i+1, code[:], result)
        code.pop()
        code.append(chr(int(number[i])*10+int(number[i+1])+96))
        all_codes(number, i+2, code[:], result)
    elif number[i] == '2':
        code.append(chr(int(number[i])+96))
        all_codes(number, i+1, code[:], result)
        code.pop()
        next_number = int(number[i+1])
        if next_number < 7:
            code.append(chr(int(number[i])*10+next_number+96))
            all_codes(number, i+2, code[:], result)
    else:
        code.append(chr(int(number[i])+96))
        all_codes(number, i+1, code[:], result)
        
    return result

number = '721023'
code = []
result = []
print(all_codes(number, 0, code, result))
print(len(result))

——————

3.9 求子集

给定一个整数数组(列表)，求该数组所代表集合的所有子集(顺序不重要)。

空集是所有集合的子集。这里用[]来代表。

Example 1

1
2
3
4
arr = [9]

output = [[]
          [9]]

Example 2

1
2
3
4
5
6
7
8
9
10
arr = [9, 12, 15]

output =  [[],
           [15],
           [12],
           [12, 15],
           [9],
           [9, 15],
           [9, 12],
           [9, 12, 15]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def subsets(arr):
    if len(arr) == 1:
        return [[], arr]
    result = []
    result.append(arr)
    result.append([])
    for i in range(len(arr)):
        if [arr[i]] not in result:
            result.append([arr[i]])
        tmp_arr = arr.copy()
        tmp_arr.pop(i)
        for sub in subsets(tmp_arr):
            if not sub in result:
                result.append(sub)
    return result

测试用例： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def test_function(test_case):
    arr = test_case[0]
    solution = test_case[1]
    
    output = subsets(arr)
        
    output.sort()
    solution.sort()
    
    if output == solution:
        print("Pass")
    else:
        print("Fail") 

arr = [9]
solution = [[], [9]]
test_case = [arr, solution]
test_function(test_case)

arr = [5, 7]
solution = [[], [7], [5], [5, 7]]
test_case = [arr, solution]
test_function(test_case)

arr = [9, 12, 15]
solution = [[], [15], [12], [12, 15], [9], [9, 15], [9, 12], [9, 12, 15]]
test_case = [arr, solution]
test_function(test_case)

rr = [9, 8, 9, 8]
solution = [[],
[8],
[9],
[9, 8],
[8, 8],
[8, 9],
[8, 9, 8],
[9, 9],
[9, 9, 8],
[9, 8, 8],
[9, 8, 9],
[9, 8, 9, 8]]
test_case = [arr, solution]
test_function(test_case)
———— ### 3.10 爬楼梯

假设有一个n阶楼梯，每次你可以爬一阶、两阶或三阶，问：你有多少种方式可以爬上去？ Example:

  • n = 3
  • output = 4

解释:

1. 1 step +  1 step + 1 step
2. 1 step + 2 steps 
3. 2 steps + 1 step
4. 3 steps

利用递归的方式实现函数staircase 

1
2
3
4
5
6
7
8
9
10
11
12
def staircase(n):
    if n == 1:
        return 1
    elif n == 2:
        return 2
    elif n == 3:
        return 4
    else:
        case_number = 0
        for i in range(1, 4):
            case_number += staircase(n-i)
        return case_number
测试用例： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def test_function(test_case):
    n = test_case[0]
    solution = test_case[1]
    output = staircase(n)
    if output == solution:
        print("Pass")
    else:
        print("Fail")

n = 3
solution = 4
test_case = [n, solution]
test_function(test_case)

n = 4
solution = 7
test_case = [n, solution]
test_function(test_case)

n = 7
solution = 44
test_case = [n, solution]
test_function(test_case)
> 增补新的更快的解决方法如下：利用caching的思想。

caching(缓存)是为了避免重计算或者从读取速度慢的内存中一次次重读数据而设置的临时的数据存储器。所以，caching(缓存)是一个允许程序执行更快的快速"查表"存储器。

利用递归实现的爬楼梯会存在一些效率的问题：

  • 如果楼梯数是5，那么程序会调用(n=4), (n=3), (n=2)
  • 计算楼梯数是4(n=4)时会调用(n=3), (n=2), (n=1)

所以就算计算小的楼梯数(5)也会出现调用多次n=3和n=2，每次调用一个函数就会多一些额外的时间。所以，综合上面的情况仔细分析可以发现如果利用缓存的思想可以节约重复计算的时间，也就是利用一个数据结构存储已经计算的结果，通过分析要计算的数值的已经计算过的结果的关系直接得到结果。

利用caching思想实现如下：

1
2
3
4
5
6
7
def staircase(n):
    solutions = [1, 2, 4]
    i = 3
    while i < n:
        solutions.append(solutions[i - 3]+solutions[i - 2]+solutions[i - 1])
        i += 1
    return solutions[n-1]

—————

3.11 目标值最后出现的位置

给定一个数组arr和一个目标值target，找到目标值target在数组arr中最后一次出现的位置。如果target不在数组中返回-1。

例如：

  1. For arr = [1, 2, 5, 5, 4] and target = 5, output = 3

  2. For arr = [1, 2, 5, 5, 4] and target = 7, output = -1

1
2
3
4
5
6
7
8
9
10
11
12
13
def last_index(arr, target):
    if len(arr) == 0:
        return -1
    elif len(arr) == 1:
        if arr[0] == target:
            return 0
        else:
            return -1
    else:
        if arr[-1] == target:
            return len(arr) - 1
        else:
            return last_index(arr[:-1], target)

测试用例： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def test_function(test_case):
    arr = test_case[0]
    target = test_case[1]
    solution = test_case[2]
    output = last_index(arr, target)
    if output == solution:
        print("Pass")
    else:
        print("False")

arr = [1, 2, 5, 5, 4]
target = 5
solution = 3
test_case = [arr, target, solution]
test_function(test_case)

arr = [1, 2, 5, 5, 4]
target = 7
solution = -1
test_case = [arr, target, solution]
test_function(test_case)

arr = [91, 19, 3, 8, 9]
target = 91
solution = 0
test_case = [arr, target, solution]
test_function(test_case)

arr = [1, 1, 1, 1, 1, 1]
target = 1
solution = 5
test_case = [arr, target, solution]
test_function(test_case)
——————

3.12 背包问题

给定n个物品，它们的价值为values，重量为weight。现在有一个包，最大承重为max_weight，求能装入物品的最大价值value。

递归实现：（从左往右，装或者不装某物品） 

1
2
3
4
5
6
7
8
9
10
11
def max_value(weight, value, i, already_value, already_weight, max_weight):
    if i == len(value):
        return already_value
    if already_weight + weight[i] > max_weight:
        return max_value(weight, value, i+1, already_value, already_weight, max_weight)
    return max(max_value(weight, value, i+1, already_value+value[i], already_weight+weight[i], max_weight),max_value(weight, value, i+1, already_value, already_weight, max_weight))
 
weight = [3, 2, 4, 7]
value = [5, 6, 3, 19]
max_weight = 11
print(max_value(weight, value, 0, 0, 0, max_weight))
上述为0/1背包问题，也就是物品数量只有一个，下面是完全背包问题，也就是物品数量有无限个，一个物品可以加任意次。

递归求解思路： 

1
2
3
4
5
6
7
8
9
10
11
def max_value(weight, value, i, already_value, already_weight, max_weight):
    if i == len(value):
        return already_value
    if already_weight + weight[i] > max_weight:
        return max_value(weight, value, i+1, already_value, already_weight, max_weight)
    return max(max_value(weight, value, i, already_value+value[i], already_weight+weight[i], max_weight),max_value(weight, value, i+1, already_value, already_weight, max_weight))
 
weight = [1, 2, 3, 4]
value = [2, 4, 4, 5]
max_weight = 5
print(max_value(weight, value, 0, 0, 0, max_weight))
### 3.13 岛问题

一个矩阵中只有0和1两种值，每个位置都可以和自己的上下左右四个位置相连，如果有一片1连在一起，这个部分叫做一个岛，求一个矩阵中有多少个岛？

举例

001010 111010 100100 000000

上面这个矩阵中有3个岛。

递归实现 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def find_island_num(m):
    island_num = 0
    for i in range(len(m)):
        for j in range(len(m[0])):
            if m[i][j] == 1: ## 可以创建岛
                build_island(m, i, j)
                island_num += 1
    return island_num

def build_island(m, i, j):
    if (i < 0) or (i > len(m) - 1) or (j < 0) or (j > len(m[0]) - 1) :
        return
    if (m[i][j] == 0) or (m[i][j] == -1):
        return
    m[i][j] = -1
    build_island(m, i-1, j)
    build_island(m, i, j-1)
    build_island(m, i, j+1)
    build_island(m, i+1, j)

m = [[0, 0, 0, 0, 0, 0, 0, 0, 0 ], 
    [0, 1, 1, 1, 1, 1, 1, 1, 0 ], 
    [0, 1, 1, 1, 0, 0, 0, 1, 0 ],
     [0, 1, 1, 0, 0, 0, 0, 1, 0 ], 
    [0, 0, 0, 0, 0, 1, 1, 1, 0 ], 
    [0, 0, 0, 0, 1, 1, 1, 0, 0 ],
    [0, 0, 0, 0, 0, 0, 0, 0, 1 ]]
print(find_island_num(m))