树

树的定义有两点：

  1. 有且仅有一个特定的称为根（root）的结点；
  2. 当结点数量>1时，其余结点可分为若干个互不相交的有限集，其中每个集合也可以看作一颗树，称之为根的子树。

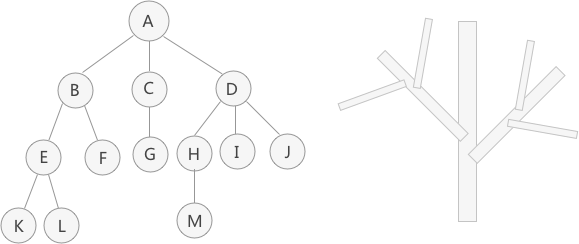
树的结点

结点：使用树结构存储的每一个数据元素都被称为“结点”。例如，上图（A）中，数据元素 A 就是一个结点；

父结点（双亲结点）、子结点和兄弟结点：对于上图（A）中的结点 A、B、C、D 来说，A 是 B、C、D 结点的父结点（也称为“双亲结点”），而 B、C、D 都是 A 结点的子结点（也称“孩子结点”）。对于 B、C、D 来说，它们都有相同的父结点，所以它们互为兄弟结点。

堂兄弟:如果两个结点的父结点虽不相同，但是它们的父结点处在同一层次上，那么这两个结点互为堂兄弟。例如，上面图（A）中，结点 G 和 E、F、H、I、J的父结点都在第二层，所以之间为堂兄弟的关系。

树根结点（简称“根结点”）：每一个非空树都有且只有一个被称为根的结点。上面图（A）中，结点 A 就是整棵树的根结点。 > 树根的判断依据为：如果一个结点没有父结点，那么这个结点就是整棵树的根结点。

叶子结点：如果结点没有任何子结点，那么此结点称为叶子结点（叶结点）。例如上面图（A）中，结点 K、L、F、G、M、I、J 都是这棵树的叶子结点。

子树和空树

子树：如上面图（A）中，整棵树的根结点为结点 A，而如果单看结点 B、E、F、K、L 组成的部分来说，也是棵树，而且节点 B 为这棵树的根结点。所以称 B、E、F、K、L 这几个结点组成的树为整棵树的子树；同样，结点 E、K、L 构成的也是一棵子树，根结点为 E。 > 注意：单个结点也是一棵树，只不过根结点就是它本身。上面图（A）中，结点 K、L、F 等都是树，且都是整棵树的子树。

空树：如果集合本身为空，那么构成的树就被称为空树。空树中没有结点。

补充：在树结构中，对于具有同一个根结点的各个子树，相互之间不能有交集。例如，上面图（A）中，除了根结点 A，其余元素又各自构成了三个子树，根结点分别为 B、C、D，这三个子树相互之间没有相同的结点。如果有，就破坏了树的结构，不能算做是一棵树。

结点的度和层次

  1. 对于一个结点，拥有的子树数（结点有多少分支）称为结点的度（Degree）。例如，上面图（A）中，根结点 A 下分出了 3 个子树，所以，结点 A 的度为 3。一棵树的度是树内各结点的度的最大值。上面图（A）表示的树中，各个结点的度的最大值为3，所以，整棵树的度的值是 3。
  2. 结点的层次：从一棵树的树根开始，树根所在层为第一层，根的孩子结点所在的层为第二层，依次类推。对于上面图（A）来说，A 结点在第一层，B、C、D 为第二层，E、F、G、H、I、J 在第三层，K、L、M 在第四层。

一棵树的深度（高度）是树中结点所在的最大的层次。图 1（A）树的深度为 4。

有序树和无序树

如果树中结点的子树从左到右看,左边和右边有顺序，这棵树称为有序树；反之称为无序树。

在有序树中，一个结点最左边的子树称为"第一个孩子"，最右边的称为"最后一个孩子"。 拿上面图（A）来说，如果是其本身是一棵有序树，则以结点 B 为根结点的子树为整棵树的第一个孩子，以结点 D 为根结点的子树为整棵树的最后一个孩子。

森林

由 m（m >= 0）个互不相交的树组成的集合被称为森林。

树可以理解为是由根结点和若干子树构成的，而这若干子树本身是一个森林，所以，树还可以理解为是由根结点和森林组成的。用一个式子表示为： Tree =（root,F） 其中，root 表示树的根结点，F 表示由 m（m >= 0）棵树组成的森林。

参考链接：https://zhuanlan.zhihu.com/p/60222380 http://c.biancheng.net/view/3383.html 选取了其中的内容，并做了部分修改。

二叉树

二叉树定义

满足以下两个条件的树就是二叉树：

  1. 本身是有序树；
  2. 树中包含的各个节点的度不能超过 2，即只能是 0、1 或者 2；

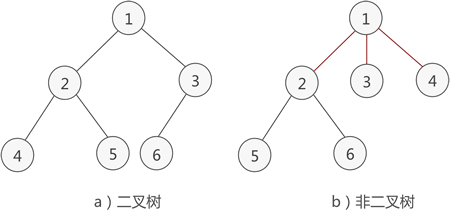
二叉树的性质

二叉树具有以下几个性质：

  1. 二叉树中，第 i 层最多有 \(2^{i-1}\) 个结点。
  2. 如果二叉树的深度为 K，那么此二叉树最多有 \(2^{2K-1}\) 个结点。
  3. 二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。

性质3的计算方法为：对于一个二叉树来说，除了度为0的叶子结点和度为2的结点，剩下的就是度为 1 的结点（设为n1），那么总结点n=n0+n1+n2。同时，对于每一个结点来说都是由其父结点分支表示的，假设树中分枝数为 B，那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的，即 B=n1+2*n2。所以，n 用另外一种方式表示为 n=n1+2*n2+1。 两种方式得到的 n 值组成一个方程组，就可以得出 n0=n2+1。

满二叉树和完全二叉树

  • 满二叉树

如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

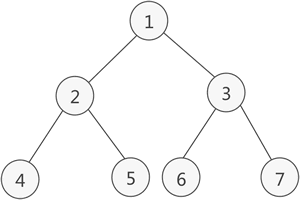
满二叉树除了满足普通二叉树的性质，还具有以下性质：

  1. 满二叉树中第 i 层的节点数为 \(2^{i-1}\) 个。
  2. 深度为 k 的满二叉树必有 \(2^{k}-1\) 个节点 ，叶子数为 \(2^{k-1}\)。
  3. 满二叉树中不存在度为1的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。
  4. 具有 n 个节点的满二叉树的深度为 \(log_{2}(n+1)\)。
  • 完全二叉树

如果二叉树中除了最后一层节点外满足为满二叉树，最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。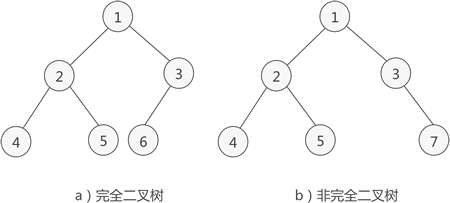

性质：

  1. n个结点的完全二叉树的深度为 \(⌊log_{2}n⌋+1\)。
  2. 如果将含有的结点按照层次从左到右依次标号（上面图a)），对于任意一个结点 i ，完全二叉树成立：当 i>1 时，父亲结点为结点[i/2]（i=1时，表示的是根结点，无父亲结点)。如果 2*i>n(总结点的个数),则结点i肯定没有左孩子（为叶子结点）；否则其左孩子是结点 2*i 。如果 2*i+1>n ，则结点 i 肯定没有右孩子；否则右孩子是结点 2*i+1 。

\(⌊log_{2}n⌋\) 表示取小于 \(log_{2}n\) 的最大整数。例如，\(⌊log_{2}4⌋ = 2\)，而 \(⌊log_{2}5⌋\) 结果也是 2。

参考链接：http://c.biancheng.net/data_structure/tree/ 部分小问题修改。

二叉树的生成

创建二叉树结点

1
2
3
4
5
class Node(object):
	def __init__(self, val=None):
		self.val = val
		self.left = None
		self.right = None

创建一颗二叉树

1
2
3
4
5
6
7
8
root = Node("apple")
Node1 = Node("banana")
Node2 = Node("cherry")
Node3= Node("dates")

root.left = Node1
root.right = Node2
Node1.left = Node3

上述创建的二叉树为：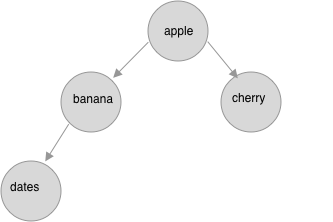

二叉树的遍历

深度优先搜索

深度优先搜索是指当前结点有子节点的话就向下搜索。深度优先搜索分为前序、中序和后序遍历三种遍历方式。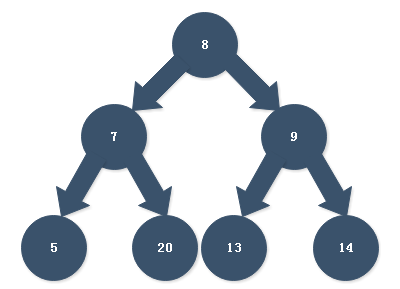

前序遍历
  • 递归实现

方法：先访问根节点，然后递归先序遍历左子树和右子树。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def preorderTraversal(root):
	preorder = []
	
	def traversal(root):
		if root == None:
			return
		## 访问根节点
		preorder.append(root.val)
		## 先序遍历左子树
		preorderTraversal(root.left)
		## 先序遍历右子树
		preorderTraversal(root.right)

	traversal(root)

	return preorder
* 迭代实现

方法：借助一个栈存放节点的右子树。如果节点不空或者栈不空进行循环，每次循环首先将当前节点（一开始是根节点 ）加入到遍历序列中去，如果节点存在右子树则将其右子树入栈，左孩子不为空时令当前节点为左孩子否则从栈顶出栈节点(右孩子)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
def preorderTraversal(root):
	node = root
	stack = []
	preorder = []
	while node != None or len(stack) > 0:
		if node != None:
			preorder.append(node.val) ## 访问节点
			if node.right != None:
				stack.append(node.right)
			node = node.left
		else:
			node = stack.pop()
	return preorder
> 前序遍历上面图中的二叉树的顺序为：8 7 5 20 9 13 14

中序遍历
  • 递归实现

方法：递归中序遍历左子树，访问根节点，递归中序遍历右子树 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def inorderTraversal(root):
	inoder = []

	def traversal(root):
		if root == None:
			return
		## 中序遍历左子树
		traversal(root.left)
		## 访问根节点
		inoder.append(root.val)
		## 中序遍历右子树
		traversal(root.right)
	
	traversal(root)
	
	return inoder
* 迭代实现

方法：借助一个栈，将当前非空节点（最开始是根节点）入栈，如果节点存在左子树，则将左子树节点入栈，继续循环判断左子树是否存在左孩子，入栈，直到不存在左孩子的节点，将当前节点从栈中弹出，并加入到遍历序列中，并将当前节点的右孩子入栈。 

1
2
3
4
5
6
7
8
9
10
11
12
13
def inoderTraversal(root):
	node = root
	inoder = []
	stack = []
	while node != None or len(stack) > 0:
		if node != None:
			stack.append(node)
			node = node.left
		else:
			node = stack.pop()
			inoder.append(node.val)
			node = node.right
	return inoder
> 中序遍历上面图中的二叉树的顺序为：5 7 20 8 13 9 14

后续遍历
  • 递归实现

方法：递归后序遍历左子树，递归后序遍历右子树，访问根节点 

1
2
3
4
5
6
7
8
9
10
11
12
13
def postorderTraversal(root):
	postorder = []

	def traversal(root):
		if root == None:
			return
		traversal(root.left)
		traversal(root.right)
		postorder.append(root.val)

	traversal(root)

	return postorder
* 迭代实现

方法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def postoderTraversal(root):
	node = root
	postorder = []
	stack = []
	pre = []
	while node != None or len(stack) > 0:
		if node != None:
			stack.append(node)
			node = node.left
		else:
			node = stack.pop()
			if node.right == None or node.right == pre:
				postorder.append(node.val)
				pre = node
				node = None
			else:
				stack.append(node)
				node = node.right
	return postorder
> 后序遍历上面图中的二叉树的顺序为：5 20 7 13 14 9 8

广度优先搜索

广度优先搜索又叫层次遍历，它从访问根节点出发，依次从左到右访问下一层结点以及下下层结点...直到最后一层。 上图的层次遍历结果为：[['apple'], ['banana', 'cherry'], ['dates']]

广度优先搜索(层次遍历)的实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def bfs(root):
	if root is None:
		return []
	queue = []
	order = []
	queue.append(root)
	while len(queue) > 0:
		level_node_num = len(queue)
		level = []
		for i in range(level_node_num):
			node = queue.pop(0)
			level.append(node.val)
			if node.left != None:
				queue.append(node.left)
			if node.right != None:
				queue.append(node.right)
		order.append(level)
	return order
### 二叉树的重要性

这个part参考： https://labuladong.github.io/algo/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E7%B3%BB%E5%88%97/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%B3%BB%E5%88%971.html

举个例子，比如说经典算法「快速排序」和「归并排序」，对于这两个算法，你有什么理解？如果你说，快速排序就是个二叉树的前序遍历，归并排序就是个二叉树的后续遍历，那么你是个算法高手了。

为什么快速排序和归并排序能和二叉树扯上关系？简单分析一下它们的算法思想和代码框架：

快速排序的逻辑是，若要对 nums[low..high] 进行排序，我们先找一个分界点 p，通过交换元素使得(左边都小右边都大) nums[low..p-1] 都小于等于 nums[p]，且 nums[p+1..high] 都大于 nums[p]，然后递归地去 nums[low..p-1] 和 nums[p+1..high] 中寻找新的分界点，最后整个数组就被排序了。

快速排序的代码如下(完整代码)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
##划分函数
def partition(arr, low, high):
	mid_value = arr[low] ## 以数组中第一个进行划分
	while low != high:
		while arr[high] > mid_value:
		def partition(arr, low, high):
    mid_value = arr[low] ## 以数组中第一个进行划分
    flag = True
    while low < high:
        if flag:
            flag = False
            while arr[high] > mid_value:
                if high > low:
                    high -= 1
                else:
                    break
            arr[low] = arr[high]
            if high > low:
                low += 1
            else:
                break
        else:
            flag = True
            while arr[low] < mid_value:
                if low < high:
                    low += 1
                else:
                    break
            arr[high] = arr[low]
            if high > low:
                high -= 1
            else:
                break
    arr[low] = mid_value ## high和low一样
    return low

## 快速排序
def quick_sort(arr, low, high):
    if low >= high:
        return
    ## 前序遍历
    p = partition(arr, low, high)
    
    quick_sort(arr, low, p-1)
    quick_sort(arr, p+1, high)

归并排序的逻辑，若要对 nums[low..high] 进行排序，我们先对 nums[low..mid] 排序，再对 nums[mid+1..high] 排序，最后把这两个有序的子数组合并，整个数组就排好序了。

归并排序的代码框架如下(不完整代码)： 

1
2
3
4
5
6
7
8
def merge_sort(arr, low, high):
	## 后序遍历的框架
	mid = (low+high) // 2
	left = merge_sort(arr, low, mid)
	right = merger_sort(arr, mid+1, high)

	result = merge(left, right)
	return result
上述归并排序就是先对左右子数组排序，然后合并。另外，这也就是分治算法的思想。

二叉树编程题

大部分来自leetcode

翻转二叉树

问题描述：翻转一棵二叉树。

示例：

python实现： 

1
2
3
4
5
6
7
8
9
10
class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return
        tmp = root.left
        root.left = root.right
        root.right = tmp
        self.invertTree(root.left)
        self.invertTree(root.right)
        return root
#### 二叉树的锯齿形层序遍历

问题陈述：给定一个二叉树，返回其节点值的锯齿形层序遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如： 给定二叉树[3,9,20,null,null,15,7],

3 /
9 20 /
15 7

返回锯齿形层序遍历如下：

[ [3], [20,9], [15,7]]

python层次遍历实现该题：

层次遍历稍微修改下即可。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        queue = []
        queue.append(root)
        flag = 1 ## 奇数从左往右
        result = []
        while len(queue) > 0:
            length = len(queue)
            level = []
            for i in range(length):
                node = queue.pop(0)
                if flag % 2 == 1:
                    level.append(node.val)
                else:
                    level.insert(0, node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            result.append(level)
            flag += 1
        return result
#### 填充每个节点的下一个右侧指针

问题陈述：给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node { int val; Node *left; Node *right; Node *next; }

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

你只能使用常量级额外空间。 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例：

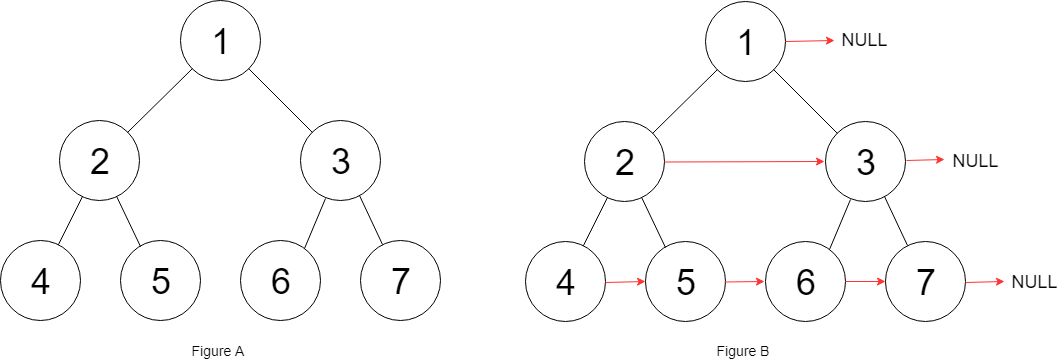
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

python层次遍历实现该题：

用到了队列，而队列是跟输入规模相关的，所以不是常量空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return
        queue = []
        queue.append(root)
        while len(queue) > 0:
            length = len(queue)
            node = None
            for i in range(length):
                if i == 0:
                    node = queue.pop(0)
                    if node.left: queue.append(node.left)
                    if node.right: queue.append(node.right)
                else:
                    tmp = queue.pop(0)
                    if tmp.left:
                        queue.append(tmp.left)
                    if tmp.right:
                        queue.append(tmp.right)
                    node.next = tmp
                    node = tmp
        return root

python递归实现： 

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return
        if root.left:
            root.left.next = root.right
            if root.next:
                root.right.next = root.next.left
        self.connect(root.left)
        self.connect(root.right)
        return root
#### 二叉树展开为链表

问题陈述：给定一个二叉树，原地(in place与空间复杂度O(1)不同)将它展开为一个单链表。

例如，给定二叉树 

1
2
3
4
5
    1
   / \
  2   5
 / \   \
3   4   6
将其展开为：

1   2  
3   4  
5   6

python递归实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def flatten(self, root: TreeNode) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        if not root: return
        node_left_flatten = self.flatten(root.left)
        node_right_flatten = self.flatten(root.right)

        if node_left_flatten:
            node = node_left_flatten
            while node.right:
                node = node.right
            node.right = node_right_flatten 
            root.right = node_left_flatten
        root.left = None
        return root
#### 二叉树的最近公共祖先

问题陈述：给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]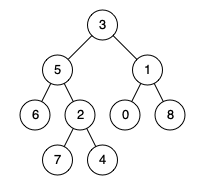

示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。  

说明: · 所有节点的值都是唯一的。 · p、q 为不同节点且均存在于给定的二叉树中。

python递归实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        node = root
        if node == None:
            return None
        if node == p or node == q:
            return node
        left = self.lowestCommonAncestor(node.left, p, q)
        right = self.lowestCommonAncestor(node.right, p, q)
        if left and right:
            return node
        elif left:
            return left
        elif right:
            return right
#### 最大二叉树

问题陈述：给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

  • 二叉树的根是数组中的最大元素。
  • 左子树是通过数组中最大值左边部分构造出的最大二叉树。
  • 右子树是通过数组中最大值右边部分构造出的最大二叉树。
  • 通过给定的数组构建最大二叉树，并且输出这个树的根节点。

示例 ：

输入：[3,2,1,6,0,5] 输出：返回下面这棵树的根节点：

6 /  
3 5   / 2 0
  1  

提示：给定的数组的大小在 [1, 1000] 之间。

python递归实现： 

1
2
3
4
5
6
7
8
9
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> TreeNode:
        if len(nums) <= 0:
            return
        root = TreeNode(max(nums))
        max_num_index = nums.index(max(nums)) 
        root.left = self.constructMaximumBinaryTree(nums[:max_num_index])
        root.right = self.constructMaximumBinaryTree(nums[max_num_index+1:])
        return root
#### 从前序与中序遍历序列构造二叉树

问题陈述：根据一棵树的前序遍历与中序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出: 前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树：

3 /
9 20 /
15 7

python递归实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        if len(preorder) == 0 or len(inorder) == 0:
            return
        if len(preorder) == 1 or len(inorder) == 1:
            return TreeNode(preorder[0])        
        root = TreeNode(preorder[0])
        root_index = inorder.index(preorder[0])
        ## 判断左右子树有为空的情况
        if root_index != 0:
            root.left = self.buildTree(preorder[1:root_index+1], inorder[:root_index]) 
        else:
            root.left = self.buildTree([], [])
        if root_index != len(inorder) - 1:
            root.right = self.buildTree(preorder[root_index+1:], inorder[root_index+1:])
        else:
            root.right = self.buildTree([], [])
        return root
#### 从中序与后序遍历序列构造二叉树

问题陈述：根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出 中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

3 /
9 20 /
15 7

python递归实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        if len(inorder) == 0 or len(postorder) == 0:
            return
        if len(inorder) == 1 or len(postorder) == 1:
            return TreeNode(inorder[0])
        root = TreeNode(postorder[-1])
        root_index = inorder.index(postorder[-1])
        if root_index != 0:
            root.left = self.buildTree(inorder[:root_index], postorder[:root_index])
        else:
            root.left = self.buildTree([], [])
        if root_index != len(inorder) - 1:
            root.right = self.buildTree(inorder[root_index+1:], postorder[root_index:-1])
        else:
            root.right = self.buildTree([], [])
        return root
#### 寻找重复子树

问题陈述:给定一棵二叉树，返回所有重复的子树。对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。

两棵树重复是指它们具有相同的结构以及相同的结点值。

示例 1：

1 /
2 3 / /
4 2 4 / 4

下面是两个重复的子树：

2 / 4

和

4 因此，你需要以列表的形式返回上述重复子树的根结点。

python实现： 每个节点为根的树进行序列化(使其成为字符串),利用节点所在树的字符串序列作为字典的键值，记录出现的值，如果值为2就将加入到结果序列。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def findDuplicateSubtrees(self, root: TreeNode) -> List[TreeNode]:
        result = []
        count = defaultdict(int)
        def collect(root):
            if not root: 
                return '#'
            # serial = "{},{},{}".format(root.val, collect(root.left), collect(root.right))
            serial = ','.join([str(root.val), collect(root.left), collect(root.right)])
            count[serial] += 1
            if count[serial] == 2:
                result.append(root)
            return serial
        collect(root)
        # for key in count.keys():
        #     print(key)
        return result
#### 二叉树的序列化与反序列化

问题陈述:序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

示例: 

你可以将以下二叉树：

1 /
2 3 /   4 5

序列化为 "[1,2,3,null,null,4,5]" 提示: 这与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

说明: 不要使用类的成员 / 全局 / 静态变量来存储状态，你的序列化和反序列化算法应该是无状态的。

  • 关于实现：问题并不困难，按自己的方式将一棵二叉树扁平化并将扁平化的序列重新建立为二叉树即可。反思后认为这个题目挣扎了很久的重要原因是把自己困在了leetcode平台的序列化二叉树的格式上，被不重要的点牵住了鼻子。

python实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.
        
        :type root: TreeNode
        :rtype: str
        """
        ## 层次遍历
        res = []
        if not root:
            return ''
        queue = []
        queue.append(root)
        position = 0
        count = 0
        while len(queue) > 0:
            length = len(queue)
            for i in range(length):
                node = queue.pop(0)
                count += 1
                if not node: 
                    res.append('null')
                else:
                    res.append(str(node.val))
                    if node.left:
                        queue.append(node.left)
                    else:
                        queue.append(None)
                    if node.right:
                        queue.append(node.right)
                    else:
                        queue.append(None)
            
        return ','.join(res)

    def deserialize(self, data):
        """Decodes your encoded data to tree.
        
        :type data: str
        :rtype: TreeNode
        """ 
        def buildBinaryTree(data):
        	## 利用扁平化的序列建二叉树
        	## 借助队列存储二叉树的节点
            if len(data) == 0:
                return
            queue = []
            root = TreeNode(int(data[0]))
            queue.append(root)
            data.pop(0)
            while len(data) > 0:
                node = queue.pop(0)
                if not node:
                    continue
                node_left = data.pop(0)
                node.left = TreeNode(int(node_left)) if node_left != 'null' else None
                node_right = data.pop(0)
                node.right = TreeNode(int(node_right)) if node_right != 'null' else None
                queue.append(node.left)
                queue.append(node.right)
            return root
        if len(data) == 0:
            return None
        data = data.split(',')
        root = buildBinaryTree(data[:])
        return root

# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))
#### 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点.

注意：两结点之间的路径长度是以它们之间边的数目表示。

递归实现 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
def depth(root):
    if not root:
        return -1
    left = depth(root.left)
    right = depth(root.right)
    if left > right:
        return left + 1 
    else:
        return right + 1
def diameterOfBinaryTree(root):
    if not root:
        return 0
    node = root
    diameter = depth(root.left) + depth(root.right) + 2
    left_diameter = diameterOfBinaryTree(node.left)     
    right_diameter = diameterOfBinaryTree(node.right)
    child_diameter = left_diameter if left_diameter > right_diameter else right_diameter
    if diameter < child_diameter:
        return child_diameter
    else:
        return diameter
#### 从根节点到目标结点的路径

给定二叉树的根节点和目标结点的值，以列表的形式返回从根节点到该节点的路径(要走的结点)。

假设二叉树中所有结点的值都不相同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class BinaryTreeNode:

    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

def is_exist(root, data):
        if not root:
            return False
        if root.data == data:
            return True
        else:
            return is_exist(root.left, data) or is_exist(root.right, data)

def path_from_root_to_node(root, data):
    path = []
    if root.data == data:
        path.append(root.data)
    else:
        if is_exist(root.left, data):
            path.append(root.data)
            path.extend(path_from_root_to_node(root.left, data))
        elif is_exist(root.right, data):
            path.append(root.data)
            path.extend(path_from_root_to_node(root.right, data))
    return path

测试用例： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
from queue import Queue

def convert_arr_to_binary_tree(arr):
    """
    Takes arr representing level-order traversal of Binary Tree 
    """
    index = 0
    length = len(arr)
    
    if length <= 0 or arr[0] == -1:
        return None

    root = BinaryTreeNode(arr[index])
    index += 1
    queue = Queue()
    queue.put(root)
    
    while not queue.empty():
        current_node = queue.get()
        left_child = arr[index]
        index += 1
        
        if left_child is not None:
            left_node = BinaryTreeNode(left_child)
            current_node.left = left_node
            queue.put(left_node)
        
        right_child = arr[index]
        index += 1
        
        if right_child is not None:
            right_node = BinaryTreeNode(right_child)
            current_node.right = right_node
            queue.put(right_node)
    return root

def test_function(test_case):
    arr = test_case[0]
    data = test_case[1]
    solution = test_case[2]
    root = convert_arr_to_binary_tree(arr)
    output = path_from_root_to_node(root, data)
    print(output)
    if output == solution:
        print("Pass")
    else:
        print("Fail")

arr = [1, 2, 3, 4, 5, None, None, None, None, None, None]
data = 5
solution = [1, 2, 5]

test_case = [arr, data, solution]
test_function(test_case)

arr = [1, 2, 3, 4, None, 5, None, None, None, None, None]
data = 5
solution = [1, 3, 5]

test_case = [arr, data, solution]
test_function(test_case)

arr = [1, 2, 3, None, None, 4, 5, 6, None, 7, 8, 9, 10, None, None, None, None, None, None, 11, None, None, None]
data = 11
solution = [1, 3, 4, 6, 10, 11]

test_case = [arr, data, solution]
test_function(test_case)

arr = [1, 2, 3, None, None, 4, 5, 6, None, 7, 8, 9, 10, None, None, None, None, None, None, 11, None, None, None]
data = 8
solution = [1, 3, 5,8]

test_case = [arr, data, solution]
test_function(test_case)
————

折纸问题

请把一张纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开。 此时折痕是凹下去的。如果继续在刚刚的基础上再从下往上对折，展开后会有三条折痕。 从上到下依次为：凹、凹、凸。

给定一个输入参数N，代表纸条从下往上连续对折N次。请从上往下打印所有折痕的方向。

例如：N=1时，打印：down

N=2时，打印：down down up。

思路：左神在讲的时候画出了精髓的图如下，然后中序遍历这个在脑海中存在的二叉树。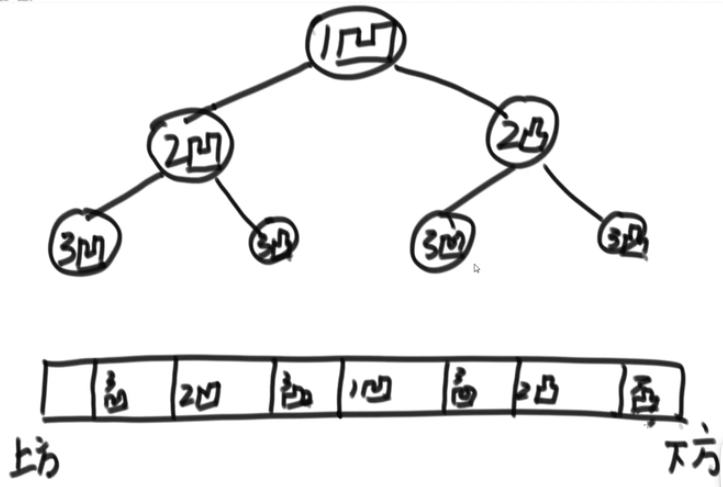

  • python实现 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    def printAllFolds(N):
        printProcess(1, N, True) ## 从第1层开始，总共N层，第一层处是凹(true)

    ## down为True是凹，False是凸
    def printProcess(i, N, down):
        if i > N:
            return
        printProcess(i+1, N, True)
        print_value = 'down' if down else 'up'
        print(print_value)
        printProcess(i+1, N, False)