二叉搜索树
二叉搜索树(BST:binary search/sort tree)又叫二叉查找树或者二叉排序树，它首先是一个二叉树，而且必须满足下面的条件： 1. 若左子树不空，则左子树上所有结点的值均小于它的根节点的值（左小） 2. 若右子树不空，则右子树上所有结点的值均大于它的根结点的值（右大） 3. 左、右子树也分别为二叉排序树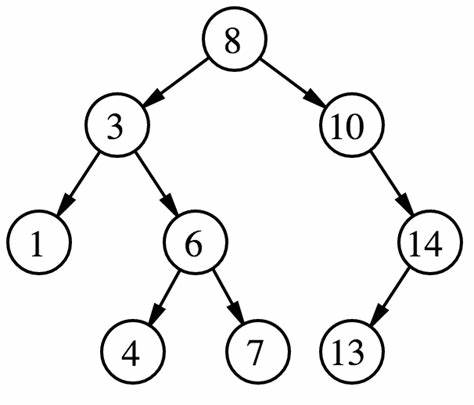 
二叉搜索树的查找
给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。 1
2
3
4
5
6
7
8
9
10
11
12def searchBST(root, val):
if root is None:
return []
node = root
while node != None:
if node.val == val:
return node
elif node.val > val:
node = node.left
else:
node = node.right
return None
给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 新值和原始二叉搜索树中的任意节点值都不同。
注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。可以返回 任意有效的结果 。
1 | class TreeNode: |
二叉搜索树的节点删除
在二叉搜索树中删除一个节点时需要考虑的情况： * 待删除节点为叶子节点：直接删除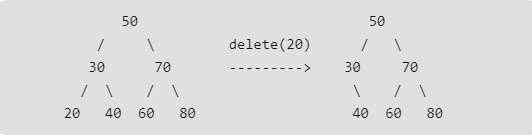 
* 待删除结点只有一个孩子：将其孩子移动到它的位置，将该结点删除 
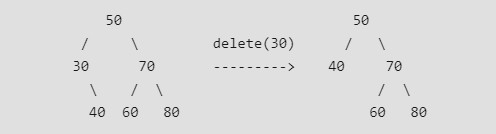* 待删除结点有两个孩子：找到其中序序列的后继结点，将待删除结点更改为其中序后继结点的值,删除该后继结点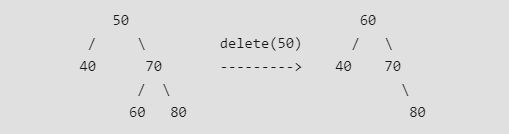 
- 递归方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44def inorderSuccessor(root, key_node):
## 返回结点的中序遍历的后继结点
node = root
pre = None
stack = []
while node or len(stack) > 0:
if node:
stack.append(node)
node = node.left
else:
node = stack.pop()
if pre == key_node:
return node
else:
pre = node
node = node.right
def deleteNode(root, key):
if root is None:
return None
node = root
if node.val == key:
if not node.left and not node.right:
## 叶子结点
return None
elif not node.left:
## 只有右孩子
return node.right
elif not node.right:
## 只有左孩子
return node.left
else:
## 左右孩子都存在
## 找到其中序遍历的后继结点
successor = self.inorderSuccessor(root, node)
## 递归删除后继结点的值 （从当前结点出发因为后继节点值在其子树上）
node = self.deleteNode(node, successor.val)
node.val = successor.val
return node
elif node.val > key:
node.left = self.deleteNode(node.left, key)
else:
node.right = self.deleteNode(node.right, key)
return root - 迭代方法： (啰嗦一句：感觉自己写的迭代的代码有点....冗长，但迭代的话就得判断很多信息欸) ### BST的相关编程题 来自leetcode.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86def inorderSuccessor(root, key_node):
## 找到其中序后继结点，处理好结点后返回其值
node = root
stack = []
pre = None
while node != None or len(stack) > 0:
if node != None:
stack.append(node)
node = node.left
else:
node = stack.pop()
if pre == key_node:
## 找到中序后继结点
val = node.val
## 如果后继结点存在右子树(不可能存在左子树，因为它是待删除结点的直接中序后继)
if node.right != None:
## 如果该后继节点为待删除结点的右孩子
if pre.right == node:
pre.right = node.right
else:
## 该后继节点不是待删除结点的右孩子
## 需要找到后继结点的父结点(栈顶结点)（父结点就是其中序遍历的后一个节点)
pre = stack[-1]
pre.left = node.right
else:
## 如果后继结点为叶子结点
## 处理后继结点(删除掉它就是让其父结点指向它的变量为None)
if pre.right == node:
pre.right = None
else:
pre = stack[-1]
pre.left = None
return val
pre = node
node = node.right
def deleteNode(root, key):
if root is None:
return None
pre = root ## 记录刚刚访问过的结点
node = root
while node != None:
if node.val == key:
## 删除
## 待删除节点为叶子节点：直接删除
if node.left == None and node.right == None:
## 删除前判断下是否为根节点
if node == root:
root = None
else:
## 父结点指向它的变量置空
if pre.val > node.val:
pre.left = None
else:
pre.right = None
return root
elif node.left == None and node.right != None:
if node == root:
root = node.right
else:
if pre.val > node.val:
pre.left = node.right
else:
pre.right = node.right
node = None
return root
elif node.left != None and node.right == None:
if node == root:
root = node.left
else:
if pre.val > node.val:
pre.left = node.left
else:
pre.right = node.left
node = None
return root
else:
node_successor_val = inorderSuccessor(root, node)
node.val = node_successor_val
return root
elif node.val > key:
pre = node
node = node.left
else:
pre = node
node = node.right
return root
二叉搜索树中第K小的元素
问题陈述：给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。
说明： 你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。
示例 1:
输入: root = [3,1,4,null,2], k = 1 3 / 1 4 2 输出: 1
示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3 5 / 3 6 / 2 4 / 1 输出: 3
进阶： 如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化kthSmallest函数？
python实现：
- 方法一：利用递归中序遍历得到排好序的序列，然后获取第k个位置上的元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
current = 0
list_node = []
def inoder(root):
if root.left != None:
inoder(root.left)
list_node.append(root.val)
if root.right != None:
inoder(root.right)
inoder(root)
return list_node[k-1] - 方法二进阶：利用迭代找到第k个元素后就返回 #### 二叉搜索树中的众数 问题描述：给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
def K_inorder(root, K_inorder):
node = root
stack = []
count = 0
while node or len(stack) > 0:
if node:
stack.append(node)
node = node.left
else:
count += 1
node = stack.pop()
if count == k:
return node.val
node = node.right
return K_inorder(root, k)
假定 BST 有如下定义：
结点左子树中所含结点的值小于等于当前结点的值 结点右子树中所含结点的值大于等于当前结点的值 左子树和右子树都是二叉搜索树 例如： 给定 BST [1,null,2,2],
1 2 / 2 返回[2].
提示：如果众数超过1个，不需考虑输出顺序
进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）
python中序遍历实现： 借助字典记录出现次数。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
from collections import defaultdict
class Solution:
def findMode(self, root: TreeNode) -> List[int]:
if not root:
return []
count = defaultdict(int)
def inorder(root):
if not root:
return
count[root.val] += 1
inorder(root.left)
inorder(root.right)
inorder(root)
max_count = max(count.values())
result = []
for item in count.items():
if item[1] == max_count:
result.append(item[0])
return result
问题描述：给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点node的新值等于原树中大于或等于 node.val 的值之和。
提醒一下，二叉搜索树满足下列约束条件：
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1：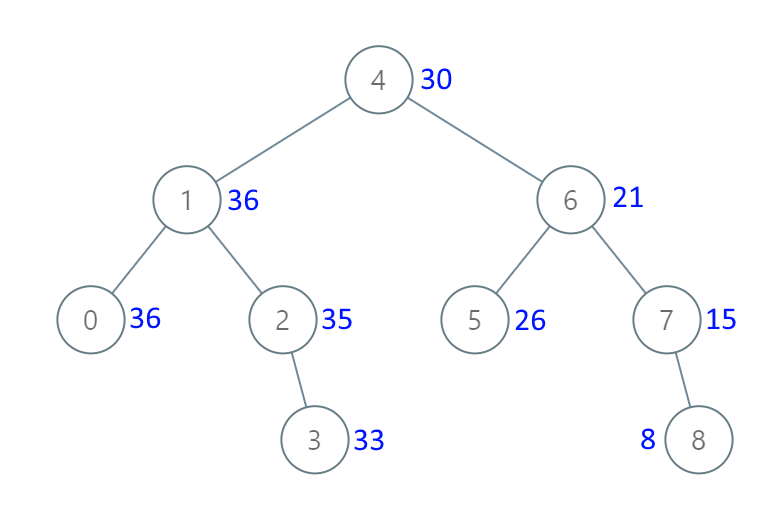 
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2：
输入：root = [0,null,1] 输出：[1,null,1]
示例 3：
输入：root = [1,0,2] 输出：[3,3,2]
示例 4：
输入：root = [3,2,4,1] 输出：[7,9,4,10]
python迭代实现： 利用迭代按照： 右 -> 中 -> 左 的方式遍历，遍历的同时加上上一个累加值。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
def GreatSumTree(root):
count = 0
node = root
stack = []
flag = True
while node or len(stack) > 0:
if node:
stack.append(node)
node = node.right
else:
node = stack.pop()
if flag: ## 最右(最大)节点
count = node.val
flag = False
else:
node.val += count
count = node.val
node = node.left
return root
return GreatSumTree(root)
平衡二叉树(AVL树--发明者的名字首字母),又称自平衡二叉查找树(self-balancing binary search tree)。平衡二叉树必定是二叉搜索树，反之则不一定。平衡二叉树满足下面的条件： 1. 左结点小于根节点，右结点大于根节点 2. 左子树和右子树的高度差不得超过1。这里通过平衡因子记录左右子树的高度差。
平衡因子：左子树的高度减去右子树的高度。由平衡二叉树的定义可知，平衡因子的取值只可能为0,1,-1,分别对应着左右子树等高，左子树比较高，右子树比较高。
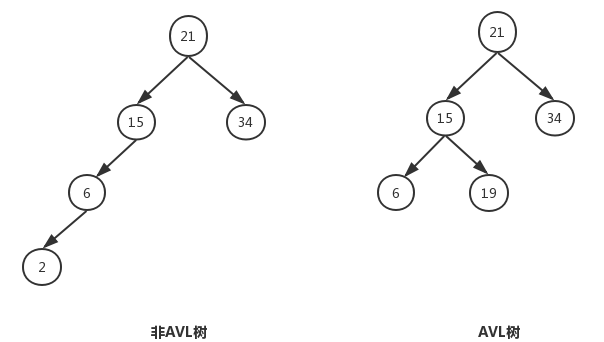
平衡二叉树的查找、插入、删除(时间复杂度都为O(log(n))) -----------------
AVL树失衡旋转的调整过程
B树
B树（Blance-Tree）平衡树，也叫作B-树。一个m阶的B树规定了： 1.根结点至少有两个子女。 2.中间节点包含k-1个元素和k个孩子，其中 m/2 <= k <= m 。 3.叶子节点包含k-1个元素，其中 m/2 <= k <= m。 4.每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分。 5.所有的叶子结点都位于同一层。 通俗理解上述定义：B树(B-树)属于平衡的多路搜索树(二叉搜索树是只有两路)，与二叉搜索树相比，B树中的节点中可以有多个值，每个值对应的子树满足左子树值均小、右子树值均大。
B树的建立(节点插入)、查找、删除
用处
在数据库索引和文件系统中大量使用B树和B+树。
B+树
B+树在B树(B-树)基础上的优化，查找性能更好。一个m阶的B+树具有如下几个特征： 1.中间节点包含有k个元素（B树中是k-1个元素）和K个子树，每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。其中 m/2 <= k <= m。 2.所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。 3.所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。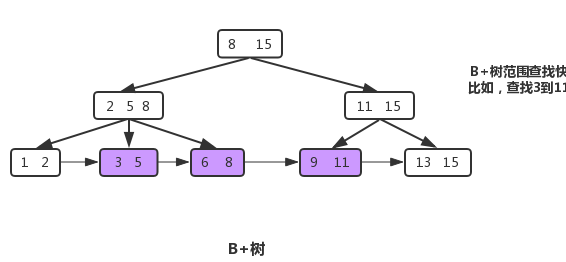 
### B+树的优点 * 单一节点存储更多的元素，使得查询的IO次数更少。 * 所有查询都要查找到叶子节点，查询性能稳定。 * 所有叶子节点形成有序链表，便于范围查询。
参考链接 1.https://blog.csdn.net/sinat_41144773/article/details/89576206?utm_medium=distribute.pc_relevant.none-task-blog-OPENSEARCH-3.not_use_machine_learn_pai&depth_1-utm_source=distribute.pc_relevant.none-task-blog-OPENSEARCH-3.not_use_machine_learn_pai
2.https://blog.csdn.net/jacke121/article/details/78268602?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-3.not_use_machine_learn_pai&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-3.not_use_machine_learn_pai
红黑树
红黑树(RB Tree, Red Black Tree)是一种含有红黑结点并能自平衡的二叉查找树。它必须满足下面性质： 性质1：每个节点要么是黑色，要么是红色。 性质2：根节点是黑色。 性质3：每个叶子节点（NIL）是黑色。 性质4：每个红色结点的两个子结点一定都是黑色。 性质5：任意一结点到每个叶子结点的路径都包含数量相同的黑结点。 从性质5又可以推出： 性质5.1：如果一个结点存在黑子结点，那么该结点肯定有两个子结点.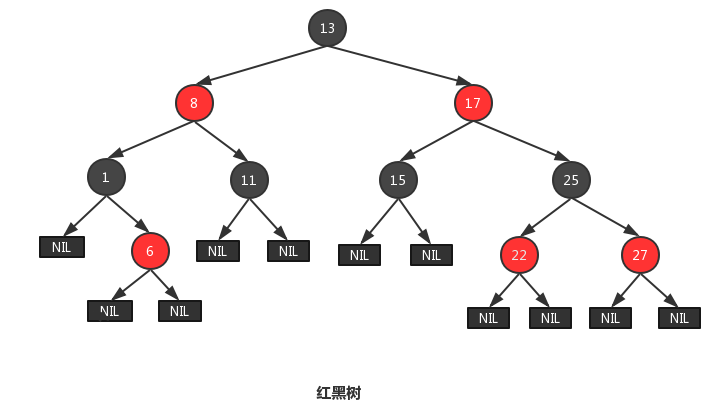 
参考链接： https://www.jianshu.com/p/e136ec79235c 推荐！