图

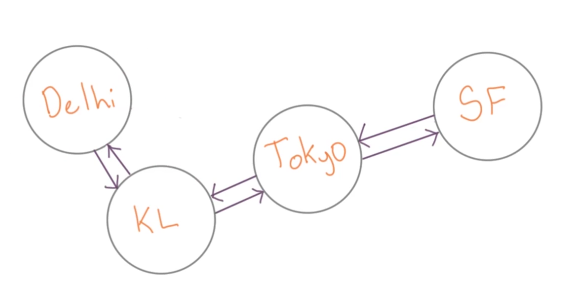
从网页或者城市之间的连接开始

在互联网上，如果想用一种数据结构来描述网页之间的连接，应该是什么样子的呢？我们知道一个网页可能被多种其他网页连接着。

在生活中，如果想要用一种数据结构来描述城市之间的连接，那么它和上述网页之间的连接所需的数据结构是一致的，都需要下图中所描绘的数据结构。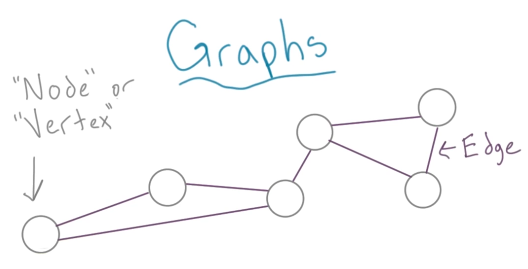

上图中描绘的数据结构就是图(Graph)。

图(Graph)

图包含顶点(vertice)和连接结点的边(edge)，顶点可以存储数据等各种信息，同样边也可以存储数据。举例来说，假设下图中每个顶点为城市，边就可以是城市与城市之间的距离。

一、关于图

1 方向(Direction)：图中顶点之间的边有出和入之分，也就是图中边存在方向，这样的图称为有向图。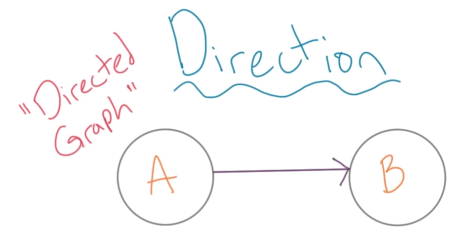

在有向图中因为边有出和入，所以一个结点可以有出边也可以有入边：

2 环(Cycle)：图中可以存在环，也就是从一个结点出发，沿着边走最后可以回到原结点。

如果无向图(图中的边没有方向)中不存在环，那么此时的图就是一棵树。(树是一种特殊的图)

如果有向图中不存在环，它就是经常使用的有向无环图(Directed Acyclic Graph, DAG)。

3 连接性(Connectivity)：顶点与其他顶点是否连接或者说是连通；还表示一个图的稳健性，如果连接性强的话，去掉一条边，整个图还是连通的，如果连接性不强，可能去掉某条边后图就不连通了，如下图所示。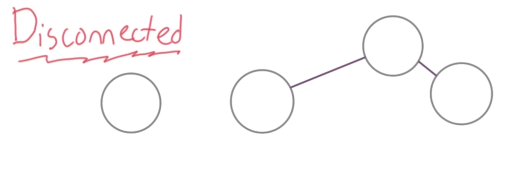

连通：如果在图中从一个顶点到达另一个顶点至少存在一条路径，则称这两个顶点是连通着的。 无向图中，连通图：任意两个顶点之间都能够连通，则此无向图称为连通图。 有向图中，强连通图：任意两个顶点满足从一个顶点到另一个顶点连通且反过来同样连通，则称此有向图为强连通图，如下图所示。

二、图的存储结构

参考：http://c.biancheng.net/view/3404.html

1 邻接矩阵(顺序存储结构)

使用数组存储图结构：一个一维数组存放图中顶点本身的数据，一个二维数组存储各顶点之间的关系也就是存储边。

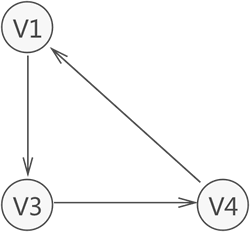
有向图和无向图的邻接矩阵存储举例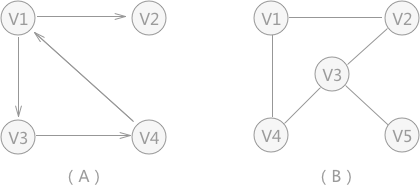： * (A)中有向图的顶点数组为：[V1, V2, V3, V4]，邻接矩阵(边的)数组为：(其中，行和列分别对应V1, V2, V3, V4) 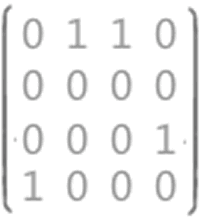邻接矩阵中的1代表存在行对应的顶点指向列对应的顶点的边。

  • (B)中无向图的顶点数组为：[V1, V2, V3, V4, V5]，邻接矩阵(边的)数组为：(其中，行和列分别对应V1, V2, V3, V4, V5) 邻接矩阵中的1代表行对应的顶点和列对应的顶点有边。因为无向图中的边没有方向，所以无向图的邻接矩阵是关于左对角线对称的。

2 邻接表(链表存储)

邻接表存储图的方式是：所有的顶点的结点存储在一维数组中，各个顶点的结点独自拥有一个链表，和该顶点有边的顶点(数组中的索引)存储在链表中。

例如，下图中左边的有向图对应右边的邻接表。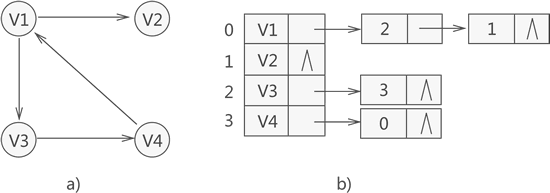

三、图的遍历

图的遍历方式包括广度优先搜索和深度优先搜索。

1 广度优先搜索

无向图中两个顶点之间的最短路径的长度，可以通过广度优先遍历得到。

对应题目见下面的LeetCode题目：单词接龙。

2 深度优先搜索

四、 编程题

1 leetcode: 127. 单词接龙

题目链接： https://leetcode-cn.com/problems/word-ladder/

参考题解：https://leetcode-cn.com/problems/word-ladder/solution/yan-du-you-xian-bian-li-shuang-xiang-yan-du-you-2/

根据题意，从benginWord开始，每次只能改变其中的一个字母而且改变了这个字母后的word还的是wordList中的，最后要变成endWord。所以，这里运用的一个技巧就是，为了防止wordList特别长，对当前词的某位用26位英文字母替换，看替换后的词是否在wordList中（注意：为了利用常数时间的查询，这里wordList在最开始要变成set——集合，这样就能利用哈希达到常数时间的查询。）

具体解法见代码。代码即思路。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#
# @lc app=leetcode.cn id=127 lang=python3
#
# [127] 单词接龙
#

# @lc code=start
class Solution:
    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        wordSet = set(wordList)
        if endWord not in wordList:
            return 0
        if beginWord in wordSet:
            wordSet.remove(beginWord)

        length_word = len(beginWord)
        queue = list()
        queue.append(beginWord)
        visited = set()
        visited.add(beginWord)
        step = 1

        while len(queue) > 0:
            level_size = len(queue)
            for i in range(level_size):
                word = queue.pop(0)
                word = list(word)
                for j in range(length_word):
                    ori = word[j]
                    for k in range(26):
                        word[j] = chr(ord('a')+k)
                        current_word = ''.join(word)
                        if current_word in wordSet:
                            if current_word == endWord:
                                return step + 1
                            if current_word not in visited:
                                queue.append(current_word)
                                visited.add(current_word)
                    word[j] = ori
            step += 1
        return 0
                                
# @lc code=end