集合(Set)

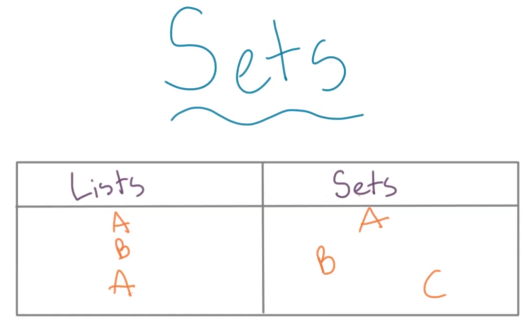
集合与列表一样用于存放数据，但是集合和列表的不同之处在于： * 集合中的元素没有顺序，它就像一个bag。所以就没有下标这种标注顺序的性质。 * 集合中的元素都是独一无二的。

映射(Maps)

映射(Maps)是一个基于集合(Set)的数据结构，就像数组(array)是基于列表(list)的数据结构。

映射(Map) = <键(Key), 值(Value)>，映射的所有键(key)就是一个集合，映射里的键就像字典中的字一样，需要独一无二，但每个字(key)可能在字典中有多个不同的解释(value)。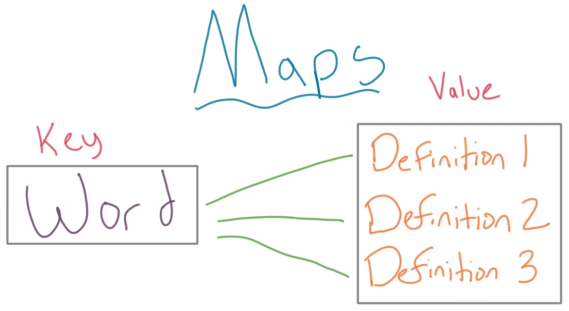

python中的映射

在python中，映射(Maps)的概念对应于一个内置的数据结构——dictionary(字典)，字典中存放键值对(key-value)。

dictionary(字典)

  1. 定义普通字典： 

    1
    2
    3
    4
    ## 定义字典
    d = {}
    ## 或者
    # d = dict()

  2. 向字典中加入键值对 key为课程，value为该课程是第几门课 

    1
    2
    3
    4
    5
    6
    d['math'] = 1
    d['English'] = 2
    d['Chinese'] = 3
    d['Physics'] = 4

    print(d)
    输出：{'math': 1, 'English': 2, 'Chinese': 3, 'Physics': 4}

  3. 查看中文课是第几门 

    1
    print(d['Chinese'])
    字典中的value可以十分灵活，你可以用很多类型作为值得类型。 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    d = dict()
    d['math'] = [1]
    d['English'] = [2]
    d['Chinese'] = [3]
    d['Physics'] = [4]
    ## 物理课又往后多加了一门。
    d['Physics'].append(5)

    print(d)
    输出：{'math': [1], 'English': [2], 'Chinese': [3], 'Physics': [4, 5]}

哈希表(Hash table)

哈希表(Hash table)查找元素为常量时间。因为它不用一个一个去看当前元素是否为目标元素，哈希表将元素和它的索引利用一个函数直接联系起来，这个函数叫做哈希函数:Hash(value) = index。

哈希函数

哈希函数的构造需要观察数据本身的情况。常见的哈希函数如下：

直接定址法

直接定址法的哈希函数为：Hash(value) = a*value + b，其中a,b为常数。这里，哈希函数为元素值的线性函数。系数a,b根据元素值的大小和分布确定。

应用举例：假设需要统计中国人口的年龄分布，以10为最小单元。今年是2020年，那么10岁以内的分布在2020-2010，20岁以内的分布在2000-2010……假设2020代表2020-2010之间的数据，那么关键字应该是2020，2010，2000……

构造上述问题的哈希函数为：$ Hash(value) = (2020-value)/10 = -value/10+202 $ ,对应哈希表为：

index value 人数(假设数据)
0 2020 43000
1 2010 23780
2 2000 34570
... ... ...

平方取中法

如果元素值的每一位都有某些数字重复出现且频率比较高的情况，可以先求元素值的平方，通过平方扩大差异，而后取中间几位数字作为最终存储的位置。

应用举例： * value1 = 1234 那么Hash(value1) = \(1234^2\) = 1522756,取227作为它的hash表地址。 * value2 = 4321 那么Hash(value2) = \(4321^2\) = 18670141,取670作为它的hash表地址。

除留余数法

除留余数法是指利用元素值对p求余得到的结果作为hash表地址，即$ Hash(value) = value%p$,其中p为不大于哈希表长度的最大质数。对p的上述限制是为了减少地址的冲突。

哈希冲突

哈希冲突是指不同的元素值(value)通过哈希函数的计算产生了相同的哈希地址。

抽屉原理：桌上有十个苹果，要把这十个苹果放到九个抽屉里，无论怎样放，我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。抽屉原理的一般含义为：“如果每个抽屉代表一个集合，每一个苹果就可以代表一个元素，假如有n+1个元素放到n个集合中去，其中必定有一个集合里至少有两个元素。”

哈希冲突的解决方案

1 开放地址法

开放地址法是指用大小为M的数组保存N个值，M>N，依靠数组中的空位解决碰撞冲突。

冲突发生时，开放地址法所利用的方式为：$ H(value, i) = (H(value, 0)+d_i) % m \(**，其中**i**是指**第几轮探测**，**\)d_i$是指第i轮探测的位置增量，m为哈希表的表长(求余表长是为了可以从位置前方继续探测)。

基于上述方式解决冲突的哈希表都叫做"开放地址"哈希表。根据探测时位置增量的不同计算方式，开放地址法包括线性探测法、平方探测法等等。

线性探测法是指当冲突发生时，顺序查看哈希表中的下一个位置，也就是位置增量\(d_i\)为1，直到找出一个空位或者查遍全表(查遍全表是因为没有空位了，也就是无法继续存储元素了。)

平方探测法的位置增量\(d_i\)依次为{\(1^2, -1^2, 2^2, -2^2, ...\)}。

对于开放地址法，不管采用什么方式探测，当散列表中的空间位置不多时冲突的概率会大大提高，为了保证哈希表的操作效率，通常会用装载因子(load factor，α)来表示空位的多少，保证哈希表中有一定比例的空闲槽位。装载因子\(α = n / m\)，其中n为实际装载的元素数量，m为哈希表表长。装载因子越大，平均查找长度(ASL)越大,通常认为α为0.75时是时间空间综合利用效率最高的情况。

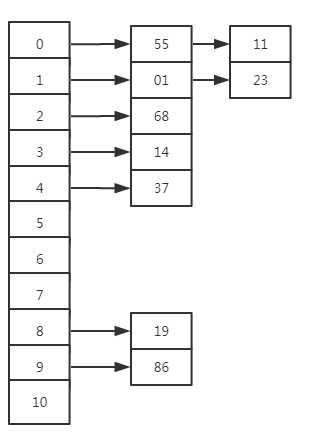
2 链地址法

链地址法是指使用一个链表数组来存储元素，当哈希函数出现冲突后依次将冲突元素加到相同数组位置的链表后。

3 再散列法

再散列法就是构造多个哈希函数，如果使用第一个哈希函数出现冲突就使用第二个哈希函数，第二个哈希函数也冲突就使用第三个哈希函数，以此类推。

哈希表的构造顺序

一般的数据结构(数组、链表、树)的平均查找长度是关于存储数据规模n的函数，但哈希表的平均查找长度与数据规模无关，它是基于装载因子α的函数。所以，当数据规模增大时，可以通过增大哈希表的表长维持装载因子α不变(确保平均查找长度不变)。那么，哈希表的构造顺序应该是： 从选择解决冲突的方法开始，考虑实际问题所给的平均查找长度的限制，确定装载因子，进而推到出哈希表表长，最后根据哈希表表长设计合适的哈希函数。

哈希表中元素的删除

对于链地址法解决冲突的哈希表，它可以直接删除元素。

对于开放地址法解决冲突的哈希表，删除元素的正确方式为将要删除元素后置入一个不存在的用于表示已删除的值(例如-1等未出现的约定的值)。如果直接对要删除的元素位置置空，那么在这个位置出现冲突而向后探测存储的元素就永远找不到了。

哈希映射(Hash Map)的实现

(哈希表hash table和哈希映射hash map概念十分相似，只不过是类的实现方式有一点不同。)

初识Hash Map

Hash Map类的大致样子是： 

1
2
3
4
5
6
7
8
9
10
11
12
13
class HashMap:
	
	def __init__(self):
		self.num_entries = 0

	def put(self, key, value):
		pass

	def get(self, key):
		pass

	def size(self):
		return self.num_entries
## 字符串的哈希函数

对于不同数据类型的元素，哈希函数是不同的。整数元素的哈希函数与字符串元素的哈希函数就是不同的。

常用的字符串哈希函数

对于一个字符串，假设为abcde，一个十分有效的哈希函数就是将其转换为以质数p为基底的数字。如下所示：\[a * p^4 + b * p^3 + c * p^2 + d * p^1 + e * p^0\]

在这里，将上面的每个字符替换为它们对应的ASCII码值。这种方式就是最流行的字符串的哈希函数。p为质数是因为能够让数字有一个好的分布，最常用的质数是31和37。

用于存储的数组起名为bucket array桶数组，桶数组中每个条目都被成为一个bucket桶，桶的位置叫做bucket index。在类中实现如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class HashMap:
	
	def __init__(self, initial_size=10):
		self.bucket_array = [None]*initial_size
		self.p = 37
		self.num_entries = 0

	def put(self, key, value):
		pass

	def get(self, key):
		pass

	def get_bucket_index(self, key):
		return self.get_hash_code(key)

	def get_hash_code(self, key):
		hash_code = 0
        i = 0
        for character in key:
            hash_code += ord(character)*pow(self.p, i)
            i += 1
        return hash_code
测试用例: 
1
2
3
4
hash_map = HashMap()

bucket_index = hash_map.get_bucket_index("abcd")
print(bucket_index)
输出：5204554 
1
2
3
4
hash_map = HashMap()

bucket_index = hash_map.get_bucket_index("bcda")
print(bucket_index)
输出：5054002

压缩函数

上个小节已经有了一个好的字符串哈希函数，但是它生成的数字很大，我们通常不能生成这么大的数组，所以我们使用另外的一个函数：compression function压缩函数，去压缩生成的哈希码到正常大小的范围。

常用的简单的方式就是求余(%)数组大小mod len(array)，将哈希码压缩到数组大小之类。通常不会新创建一个压缩函数，基本上都是直接在生成哈希码的时候加上取余进行压缩。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class HashMap:
	
	def __init__(self, initial_size=10):
		self.bucket_array = [None]*initial_size
		self.p = 37
		self.num_entries = 0

	def put(self, key, value):
		pass

	def get(self, key):
		pass

	def get_bucket_index(self, key):
		return self.get_hash_code(key)

	def get_hash_code(self, key):
		hash_code = 0
        i = 0
        for character in key:
            hash_code += ord(character)*pow(self.p, i)
            i += 1
        return hash_code%len(self.bucket_array) ## compression

冲突处理

常用的冲突处理办法有开放地址法与链地址法。这里实现HashMap的put和get函数利用链地址法解决冲突。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class LinkedListNode:

	def __init__(self, key, value):
		self.key = key
		self.value = value
		self.next = None

class HashMap:

	def __init__(self, initial_size=10):
		self.bucket_arry = [None]*initial_size
		self.p = 31
		self.num_entries = 0

	def put(self, key, value):
		index = self.get_bucket_index(key)
		if not self.bucket_array[index]:
			self.bucket_arrray[index] = LinkedListNode(key, value)
			self.num_entries += 1
		else:
			node = self.bucket_array[index]
			while node.next:
				if node.key == key: ##检查是否key已经存在 更新value
					node.value = value
					break
				node = node.next
			if node.value != value:
				node.next = LinkedListNode(key, value)
				self.num_entries += 1
	
	def get(self, key):
		index = self.get_bucket_index(key)
		node = self.bucket_array[index]
		while node.key != key:
			if node.next:
				node = node.next
			else:
				return None
		return node.value

	def get_bucket_index(self, key):
		return self.get_hash_code(key)

	def get_hash_code(self, key):
		hash_code = 0
        i = 0
        for character in key:
            hash_code += ord(character)*pow(self.p, i)
            i += 1
        return hash_code%len(self.bucket_array) ## compression

测试用例： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
hash_map = HashMap()

hash_map.put("one", 1)
hash_map.put("two", 2)
hash_map.put("three", 3)
hash_map.put("neo", 11)

print("size: {}".format(hash_map.size()))


print("one: {}".format(hash_map.get("one")))
print("neo: {}".format(hash_map.get("neo")))
print("three: {}".format(hash_map.get("three")))
print("size: {}".format(hash_map.size()))
输出: size: 4 one: 1 neo: 11 three: 3 size: 4

时间复杂度分析与Rehashing

1. put操作时间复杂度分析

利用数组实现哈希映射是因为数组提供\(O(1)\)时间复杂度的put和get操作。在哈希映射中的put操作中计算字符串的bucket_index(哈希码)时遍历了字符串，但是对于输入数据(这里是字符串)的总量(一般在\(10^5\))来说，每个字符串的长度可以说是非常小，所以分析时间复杂度时这里可以忽略哈希计算的时间。

所以，整个的时间复杂度依赖冲突发生时链表的遍历。冲突依赖装载因子，假设有n个条目b个桶(bucket)或者叫槽位，所以时间复杂度为\(O(\dfrac{n}{b})\)。

一般来说，装载因子α(上面有解释)不大于0.7。

当装载因子大于0.7时需要增加bucket_array的长度，同样就需要重新计算Hash Map中条目的哈希索引(hash index)，这是因为计算哈希索引时求余了数组的长度，现在数组长度变化了需要对它们重新计算。这个过程就叫Rehashing。

Rehashing: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class LinkedListNode:
    
    def __init__(self, key, value):
        self.key = key
        self.value = value
        self.next = None

class HashMap:
    
    def __init__(self, initial_size = 10):
        self.bucket_array = [None for _ in range(initial_size)]
        self.p = 31
        self.num_entries = 0
    
    def put(self, key, value):
        index = self.get_bucket_index(key)
        if not self.bucket_array[index]:
            self.bucket_array[index] = LinkedListNode(key, value)
            self.num_entries += 1
        else:
            node = self.bucket_array[index]
            while node.next:
                if node.key == key: ## 检查是否key已经存在 更新value
                    node.value = value
                    break
                node = node.next
            if node.value != value:
                node.next = LinkedListNode(key, value)
                self.num_entries += 1
        ## 确认装载因子
        alpha = self.num_entries / len(self.bucket_array)
        if alpha > 0.7:
            self._rehash()

    def get(self, key):
        index = self.get_bucket_index(key)
        node = self.bucket_array[index]
        while node.key != key:
            if node.next:
                node = node.next
            else:
                return None
        return node.value

    def get_bucket_index(self, key):
        return self.get_hash_code(key)
    
    def get_hash_code(self, key):
        hash_code = 0
        i = 0
        for character in key:
            hash_code += ord(character)*pow(self.p, i)
            i += 1
        return hash_code%len(self.bucket_array)
    
    def size(self):
        return self.num_entries
    
    def _rehash(self):
        new_size = 2*len(self.bucket_array)
        old_array = self.bucket_array
        self.bucket_array = [None]*new_size
        self.num_entries = 0
        for entry_node in old_array:
            node = entry_node
            ## 链表上所有值
            while node:
                self.put(node.key, node.value)
                node = node.next
2 get和delete操作时间复杂度

get和delete操作的逻辑是一样的，它们都是O(1)的时间复杂度。

delete: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
class LinkedListNode:
    
    def __init__(self, key, value):
        self.key = key
        self.value = value
        self.next = None

class HashMap:
    
    def __init__(self, initial_size = 10):
        self.bucket_array = [None for _ in range(initial_size)]
        self.p = 31
        self.num_entries = 0
    
    def put(self, key, value):
        index = self.get_bucket_index(key)
        if not self.bucket_array[index]:
            self.bucket_array[index] = LinkedListNode(key, value)
            self.num_entries += 1
        else:
            node = self.bucket_array[index]
            while node.next:
                if node.key == key: ## 检查是否key已经存在 更新value
                    node.value = value
                    break
                node = node.next
            if node.value != value:
                node.next = LinkedListNode(key, value)
                self.num_entries += 1
        ## 确认装载因子
        alpha = self.num_entries / len(self.bucket_array)
        if alpha > 0.7:
            self._rehash()

    def get(self, key):
        index = self.get_bucket_index(key)
        node = self.bucket_array[index]
        while node.key != key:
            if node.next:
                node = node.next
            else:
                return None
        return node.value

    def get_bucket_index(self, key):
        return self.get_hash_code(key)
    
    def get_hash_code(self, key):
        hash_code = 0
        i = 0
        for character in key:
            hash_code += ord(character)*pow(self.p, i)
            i += 1
        return hash_code%len(self.bucket_array)
    
    def size(self):
        return self.num_entries
    
    def _rehash(self):
        new_size = 2*len(self.bucket_array)
        old_array = self.bucket_array
        self.bucket_array = [None]*new_size
        self.num_entries = 0
        for entry_node in old_array:
            node = entry_node
            ## 链表上所有值
            while node:
                self.put(node.key, node.value)
                node = node.next
                
    def delete(self, key):
        index = self.get_bucket_index(key)
        node = self.bucket_array[index]
        pre = node
        while node.key != key:
            if node.next:
                pre = node
                node = node.next
            else:
                return None
        if pre != node:
            pre.next = node.next
        else: ## 第一个节点
            self.bucket_array[index] = node.next
        self.num_entries -= 1
测试用例： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
hash_map = HashMap(7)

hash_map.put("one", 1)
hash_map.put("two", 2)
hash_map.put("three", 3)
hash_map.put("neo", 11)

print("size: {}".format(hash_map.size()))


print("one: {}".format(hash_map.get("one")))
print("neo: {}".format(hash_map.get("neo")))
print("three: {}".format(hash_map.get("three")))
print("size: {}".format(hash_map.size()))

hash_map.delete("one")

print(hash_map.get("one"))
print(hash_map.size())
输出：size: 4 one: 1 neo: 11 three: 3 size: 4 AttributeError Traceback (most recent call last) ..... AttributeError: 'NoneType' object has no attribute 'key'

python中的字典与集合

python中的字典类型(dict)本质上是一个哈希表(python会保证数组中至少有三分之一是空白的），字典(dict)的每个键都会占用数组中一个条目，而一个条目包含了两部分：键的引用和值的引用。

当我们想要向字典中存入一个键值对的时候，首先会计算键的哈希值(使用python的中的hash()函数)，但是，不是所有的python对象都可以使用hash()来获取哈希值(所以，有的python对象不能作为dict的键。例如：列表)。

set(集合)的本质也是哈希表，所以，有的python对象因为不能hash()求哈希值进而不能作为set元素(例如，列表)。因为set(集合)只存储元素，所以哈希表中的每个条目只存储元素一部分。

python利用开放地址法来解决哈希冲突。

字典利用实例1

这里使用字典是为了利用哈希求值的常数时间。

问题陈述：给定一个整数的输入列表input_list和一个目标值target，返回列表中两个整数之和为target的索引。

python字典实现： 

1
2
3
4
5
6
7
def pair_sum(input_list, target):
	dict_index = dict()
	for index, element in enumerate(input_list):
		if target - element in dict_index:
			print(index, dict_index[target-element])
		else:
			dict_index[element] = index
测试用例： 
1
2
3
4
5
6
7
8
9
10
11
12
13
def test_function(test_case):
    output = pair_sum_to_zero(test_case[0], test_case[1])
    print(output)
    if sorted(output) == test_case[2]:
        print("Pass")
    else:
        print("Fail")

test_case_1 = [[1, 5, 9, 7], 8, [0, 3]]
test_function(test_case_1)

test_case_2 = [[10, 5, 9, 8, 12, 1, 16, 6], 16, [0, 7]]
test_function(test_case_2)
### 字典利用实例2

问题陈述：给定一个整数列表，求出其中最长的连续的数字序列。要求是在O(n)时间复杂度内实现。 例如：给定整数列表5, 4, 7, 10, 1, 3, 55, 2, 返回1, 2, 3, 4, 5。

python实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def longest_consecutive_subsequence(input_list):
    input_dict = dict()
    for i, element in enumerate(input_list):
        input_dict[element] = i
        
    max_length = 0
    max_start = -1
    
    for index, element in enumerate(input_list):
        current_start = index
        input_dict[element] = -1
        current_count = 1
        
        ## 向大的方向查找
        current_element = element + 1
        while current_element in input_dict and input_dict[current_element] != -1:
            current_count += 1
            input_dict[current_element] = -1
            current_element += 1
        
        ## 向小的方向查找
        current_element = element - 1
        while current_element in input_dict and input_dict[current_element] != -1:
            current_start = input_dict[current_element]
            current_count += 1
            input_dict[current_element] = -1
            current_element -= 1
        
        if current_count > max_length:
            max_length = current_count
            max_start = current_start
        elif current_count == max_length:
            if current_start < max_start:
                max_length = current_count
                max_start = current_start
    start = input_list[max_start]
    return [element for element in range(start,start+max_length)]
测试用例： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def test_function(test_case):
    output = longest_consecutive_subsequence(test_case[0])
    print(output)
    if output == test_case[1]:
        print("Pass")
    else:
        print("Fail")

test_case_1 = [[5, 4, 7, 10, 1, 3, 55, 2], [1, 2, 3, 4, 5]]
test_function(test_case_1)

test_case_2 = [[2, 12, 9, 16, 10, 5, 3, 20, 25, 11, 1, 8, 6 ], [8, 9, 10, 11, 12]]
test_function(test_case_2)

test_case_3 = [[0, 1, 2, 3, 4], [0, 1, 2, 3, 4]]
test_function(test_case_3)