LRU
LRU(Least Recently Used, 最近最少使用算法)是指当空间满了又有新的数据到来时淘汰数据的算法,它根据数据的历史访问记录把当前最久没有被访问的数据淘汰。
LRU依据的思想是:“如果数据最近被访问过,那么下一次被访问的几率更高”。也就是从另一个角度来看:“如果一个数据最近很久都没有被访问过,那么它在将来被访问的几率就很小”。
LRU的实现方式
1 数组
- 用一个数组来存储数据,给每一个数据项标记一个访问的时间戳。
- 每次插入新的数据时,先把原来数组中存在的数据的时间戳自增,并将新数据的时间戳置为0(最小值)插入到数组中。当数组的空间已满时,将时间戳最大的数据淘汰。
- 每次访问数组中的数据项的时候,将被访问的数据的时间戳置为0(最小值)。
2 链表
- 利用一个链表来存储数据。
- 每次插入新的数据的时候,将要插入的数据插入到链表的头部。当链表满的时候(按理说链表不会满,这里是指达到设定的长度等等),就将链表尾部的数据淘汰。
- 每次访问数据时,将被访问的数据移到链表的头部。
3 哈希表和双向链表实现
这一种实现方式时比上面两种实现方式更优,不需要维护时间戳,插入、淘汰和访问数据的时间复杂度都是常数。
- 使用哈希表存储键值对,其中键(key)就是数据,值(value)是指向存储了数据(也就是key)的双向链表节点的变量。
- 双向链表(或者说环形双向链表)用于存储数据,头部为最近访问节点。
- 每次插入的数据时,如果数据(key)不存在,则新建节点置于链表开头。如果数据已经存在,更新节点的值,同时将节点值与链表头部。当链表长度超标时,将处于尾部的节点淘汰。
- 每次访问数据(key)时,如果key存在,则将其节点移动到链表头部。
上述实现可以自己写出,或者利用python中的OrderedDict数据结构,它是一个“有序”的哈希表,其实它是用哈希表和(环形)双向链表实现的。OrderedDict将最新数据置于末尾。
LRU拓展
1 LRU-K
LRU-K中的K代表最近使用的次数,LRU可以认为是LRU-1。LRU-K的主要目的是为了解决LRU“缓存污染”的问题(具体含义见下面 缓存 部分),其核心思想是“数据最近被访问过1次”变成“数据最近被访问过K次”那么将来被访问的概率会更高。
LRU-K与LRU的区别是LRU-K多了一个数据访问历史记录队列(注意:访问历史队列并不是缓存队列,所以是不保存数据本身的,只是保存对数据的访问记录---数据此时依旧在原始存储中),队列中维护者数据被访问的次数以及时间戳,只有当这个数据被访问的次数不小于K值时,才会从历史记录队列中删除,然后把数据加入到缓存队列中去。 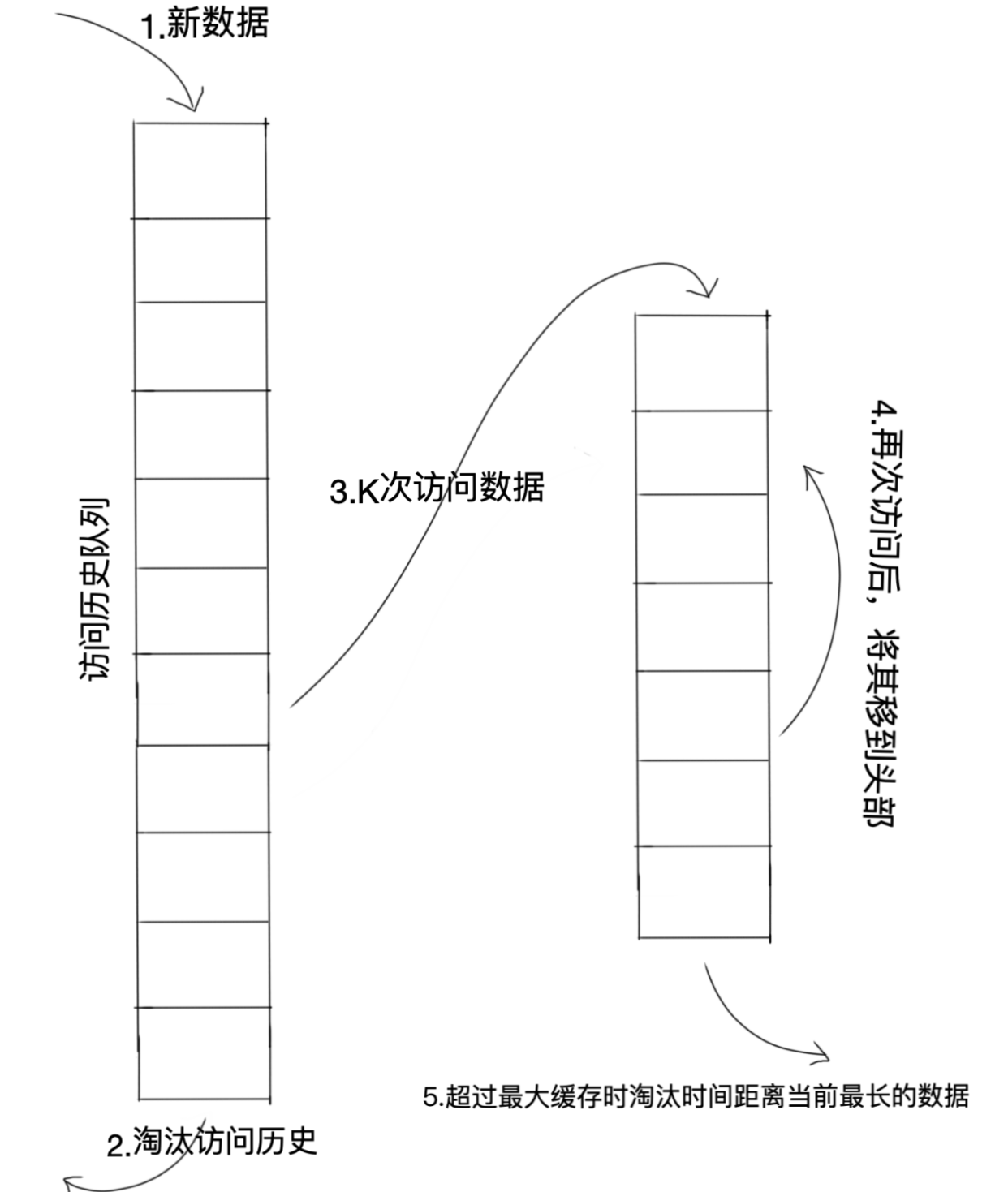
实际应用中综合各种因素后最优的选择时LRU-2。LUR-3或者更大的K值会使命中率高,但是适应性差,即一旦访问模式发生改变,需要大量的新数据访问才能将历史热点访问记录清除掉。
2 Two queues算法
Two queues算法类似于LRU-2,不同点在于Two queues算法将LRU-2算法中的访问历史队列(不在缓存中)改为一个FIFO缓存队列(按照FIFO规则淘汰数据),另外一个为LRU缓存队列。
当数据第一次被访问时,Two queues算法将数据缓存到FIFO队列中。当数据第二次被访问时,将数据从FIFO队列中移到LRU队列中去,两个队列按照自己的方式淘汰数据。 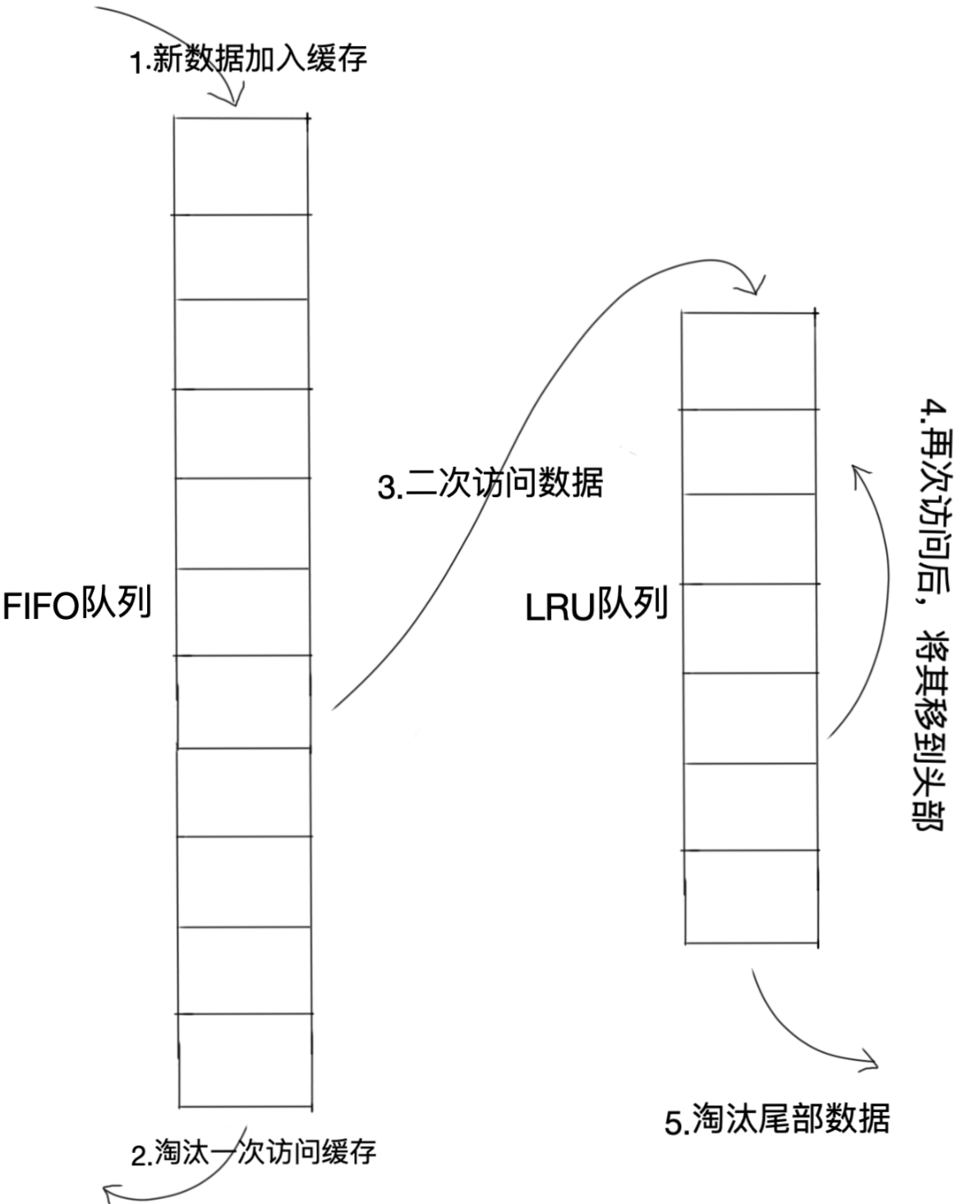
3 Multi-Queues算法
Multi-Queues算法根据访问频率将数据放入到多个队列,不同的队列有不同的优先级。它的核心思想是“优先缓存访问次数多的数据”。
Multi-Queues实现:它将缓存划分为多个LRU队列,每个队列对应不同的访问优先级(访问优先级是根据访问次数计算出来的)。例如下图Q0,Q1,Q2...Q所示,Q-history保存从缓存 中淘汰的数据,记录了数据的索引和引用次数。
算法流程:新插入的数据放入Q0,每个队列按照LRU管理,再次访问的数据移动到头部。当数据的访问次数达到一定次数,提升优先级,将数据从当前队列删除加入到高一级队列的头部。为了防止高优先级数据永远不被淘汰,当数据在指定时间内没有被访问过时,需要降低它的优先级,将数据从当前队列删除,移到低一级的队列的头部。淘汰数据时,从最低一级队列开始按照LRU淘汰,淘汰的数据的索引加入到Q-history头部(按照LRU淘汰)。如果数据在Q-history中被重新访问,则重新计算优先级移动到目标队列的头部。
LRU cache(缓存)
cache(缓存)
由于缓存的读取速度比非缓存要快很多,所以在高性能场景下系统在读取数据时,首先从缓存中查找需要的数据,如果找到了则直接读取,如果未找到则从内存或硬盘中查找,再将查找到的数据存入缓存以备下次再用。
缓存包含的“查表”操作(get())和put()/set()操作需要很快的速度。当执行get()操作时,如果数据就在缓存中,那么这就是cache hit(缓存命中),相反就是cache miss(缓存未命中)。
设计缓存时有空间的上限,如果缓存满了在新增数据时需要淘汰机制来删除数据。淘汰机制使用的就是LRU。
缓存污染会在缓存淘汰数据时出现,它是指系统将不常用的数据从内存移到缓存,造成常用数据的挤出,降低缓存效率的现象。
设计cache
问题陈述:
来源leetcode
设计和实现一个 LRU (最近最少使用) 缓存机制 。 实现 LRUCache 类: * LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存 * int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。 * void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。 进阶:你是否可以在 O(1) 时间复杂度内完成这两种操作?
python实现
利用OrderedDict,它将新的元素置于末尾。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27from collections import OrderedDict
class LRUCache:
def __init__(self, capacity: int):
self.cache = OrderedDict()
self.capacity = capacity
def get(self, key: int) -> int:
try: ## 如果值存在cache中
value = self.cache.pop(key)
## OrderedDict的最新数据置于末尾
self.cache[key] = value
return value
except KeyError:
return -1
def put(self, key: int, value: int) -> None:
if key in self.cache:
self.cache.pop(key)
self.cache[key] = value
else:
if len(self.cache) < self.capacity:
self.cache[key] = value
else: ## 没有空间了 需要淘汰元素
## 末尾是最新的 头部是最久的 所以删除头部元素
self.cache.popitem(last=False)
self.cache[key] = value