编程题-柱状图中最大的矩形

来源：leetcode: 柱状图中最大的矩形 最大矩形

问题陈述

给定n个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例

输入: [2,1,5,6,2,3]
输出: 10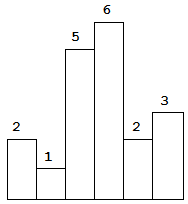

以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

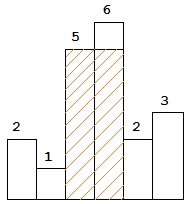图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

求解

参考别人的解法 总结出自己的解法和代码如下。

1 暴力解法

求可能的矩形的最大面积，可以枚举以每个柱形为高度的最大矩形的面积，最后选择最大的矩形面积。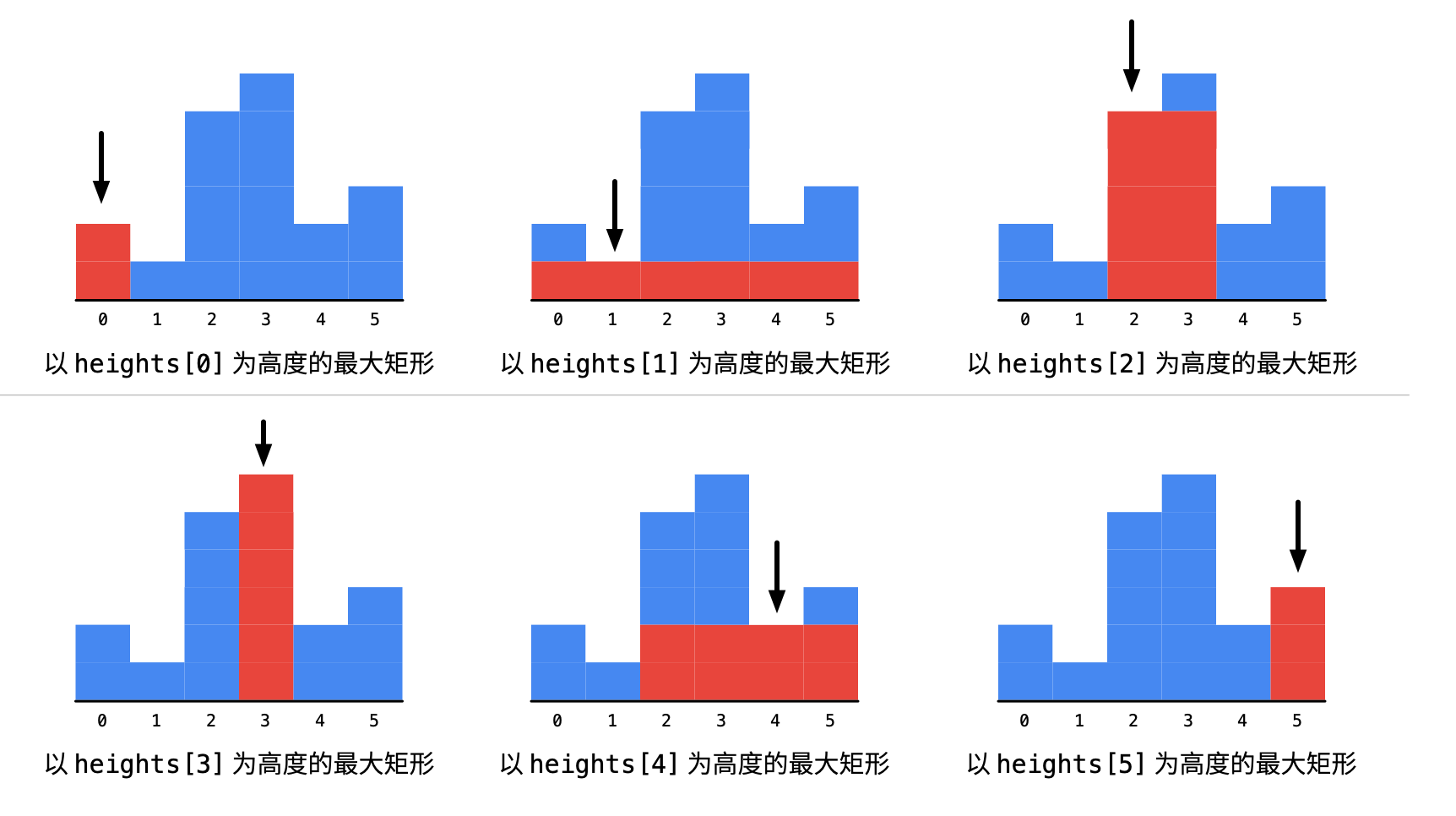

python实现： (94 / 96 个通过测试用例：对于很长的测试用例，python暴力解法代码时间通不过) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def largestRectangleArea(self, heights):
    	max_area = 0
    	for i in range(len(heights)):
    		## 向左延伸
    		left = i-1
    		while left >= 0:
    			if heights[left] >= heights[i]:
    				left -= 1
    			else: break
    		right = i+1
    		## 向右延伸
    		while right < len(heights):
    			if heights[right] >= heights[i]:
    				right += 1
    			else: break

    		area = (right - left - 1)*heights[i]
    		max_area = max(area, max_area)
    	return max_area
### 2 单调栈解法

单调栈就是一种从栈底到栈顶元素依次递增或递减的栈。这里利用存放柱子的高度的递增的栈(这里是后一个的元素大于等于前一个元素)。

思路就是：将柱子高度依次尝试入栈，入栈前首先比较它与栈顶柱子高度的大小： * 如果大于栈顶柱子高度直接入栈。 * 如果小于栈顶柱子高度，那么需要从栈顶开始依次出栈(出栈时的操作在后面)直到遇到比尝试入栈的柱子小的柱子。出栈时的操作：记录出栈柱子高度，判断与上一已经出栈的柱子高度的大小： - 如果小，那么此时上一已经出栈的柱子所能延伸的最大面积就可以计算出来了：面积 = （后面尝试入栈的柱子列表索引 - 当前出栈柱子的列表索引 - 1)*柱子高度 - 如果相等，那么继续。(继续出栈向前面的柱子延伸)

可以先去看上面参考的别人的解法,看完之后结合这里的总结应该能够完全明白。

为了保证上面计算面积的时候所有柱子都一一致(最左边和最右边这两种特殊的)，在最左边和最右边增加高度为-1的柱子(问题输入的为非负整数)。

python实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def largestRectangleArea(self, heights):
        heights.insert(0, -1)
        heights.append(-1)
        stack = [0]
        max_area = 0
        for i in range(1, len(heights)):
            if heights[i] >= heights[stack[-1]]:
                stack.append(i)
            else:
                while heights[stack[-1]] > heights[i]:
                    top_height = heights[stack.pop()]
                    while heights[stack[-1]] == top_height:
                        stack.pop()
                    area = (i - stack[-1] - 1)*top_height
                    max_area = max(area, max_area)
                stack.append(i)
        return max_area
# 编程题-最大矩形

问题陈述

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例

示例 1：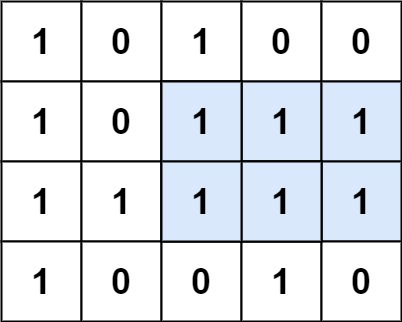

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出：6 解释：最大矩形如上图所示。

示例 2：

输入：matrix = [] 输出：0

示例 3：

输入：matrix = [["0"]] 输出：0

示例 4：

输入：matrix = [["1"]] 输出：1

示例 5：

输入：matrix = [["0","0"]] 输出：0  

提示：

rows == matrix.length cols == matrix[0].length 0 <= row, cols <= 200 matrix[i][j] 为 '0' 或 '1'

求解

已有上面一道编程题的经验，那么在求本题中的最大矩形时可以通过思考得出解法：对于二进制矩阵的每一行，求其向上形成的柱状图的最大矩形面积： * 如果当前行的某个元素为0，则无法向上成为柱子。 * 如果当前行某个元素为1，那么向上计算它的柱子的高度。 - 计算这行所有的柱子高度后通过单调栈(参考上面一题的解法)进行面积求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution:
	def largestRectangleArea(self, heights):
        heights.insert(0, -1)
        heights.append(-1)
        stack = [0]
        max_area = 0
        for i in range(1, len(heights)):
            if heights[i] >= heights[stack[-1]]:
                stack.append(i)
            else:
                while heights[stack[-1]] > heights[i]:
                    top_height = heights[stack.pop()]
                    while heights[stack[-1]] == top_height:
                        stack.pop()
                    area = (i - stack[-1] - 1)*top_height
                    max_area = max(area, max_area)
                stack.append(i)
        return max_area

    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        max_area = 0
        
        ## 每一行
        for i in range(len(matrix)):
        	## 计算每行向上形成的柱子高度
        	heights = []
        	for j in range(len(matrix[i])):
        		current_height = 0
        		index = i
        		while matrix[index][j] == "1":
        			current_height += 1
        			if index > 0:
        				index -= 1
        			else: break
        		heights.append(current_height)
        	## 计算面积
        	area = self.largestRectangleArea(heights)
        	max_area = max(area, max_area)
       	return max_area