动态规划 (Dynamic Programming)

参考链接：https://www.zhihu.com/question/23995189/answer/613096905

0 从凑钱开始

凑钱问题

现在有1、5、10、20、50、100元面值的钞票，目标是用尽量少的钞票凑出某个金额Target。

尝试解决凑钱问题

既然要用尽量少的钞票，那么我们在凑钱的时候就先从面值大的开始，当面值大的钞票超过要凑的金额时选择面值小的钞票，依次下去。举例来说，如果要凑666元，那么先取100(还差566)，再取100(重复5次)，最后取出6张100元后(还差66)，开始取50(还差16)，开始取10(还差6)，开始取5(还差1)，开始取1(还差0)，结束。

上述的策略(从大的面值开始，直到超标后开始选择小的面值)为贪心策略，贪心策略关注当前这一步做出来最优选择，所以贪心是一种只考虑眼前情况的策略，对于有些场景贪心策略的方案可能是低效的，例如，只有面值为1、5、11的钞票，需要凑出15元，贪心策略的步骤是：先拿一张11(还差4元)，再拿4张1元，一种拿了五张。但是，正确的策略是：拿三张5元钞票。

所以，更好的策略不能只考虑当前，需要考虑全局的情况。如果选择考虑所有情况的暴力枚举，把所有能凑出15元的方案都找到，然后选择一个最少张的方案，缺点很明显就是时间复杂度很高。那么，如果尝试取11，接下来就是Target=4的情况；如果尝试取5，接下来就是Target=10的情况；如果尝试取1，接下来就是Target=14的情况。可以看出，做出一个选择后，问题重新变成：给定Target，凑出它的最少钞票数是多少张。上述过程是把原问题拆解成了子问题，变化的(状态)是Target值。

由上面的分析可知：假设\(f(n)\)为凑出n所需的最少钞票数，那么\(f(15) = min{f(15-1), f(15-5), f(15-11)} + 1\).一般情况即为：\(f(n) = min{f(n-1), f(n-5), f(n-11)} + 1\)

所以我们只要从小到大，把\(f(1)\)、\(f(2)\)、\(f(3)\)、\(f(4)\)、\(f(5)\)...计算出来，等到了\(f(n)\)，结果就直接出来了。python参考代码如下： 

1
2
3
4
5
6
7
8
9
10
11
12
def money(target):
	f = [0 for i in range(target +1)]
	for i in range(1, target+1):
		cost = 100000 ## 假设这个值为不会取到的最大值
		if i - 1 >= 0:
			cost = min(cost, f[i-1] + 1)
		if i - 5 >= 0:
			cost = min(cost, f[i-5] + 1)
		if i - 11 >= 0:
			cost = min(cost, f[i-11] + 1)
		f[i] = cost
	return f[target]
时间复杂度只有\(O(n)\)，比起贪心策略，上述方式分别考虑了取出1、5、11的代价，所以避免了只关注当前最优。

之所以能像上面那样解决是因为问题的性质：如果要求f(n)，只需知道几个更小的f(c)。求解f(c)成为求解f(n)的子问题。这就是动态规划(Dynamic programming)。

众所周知，Dynamic programming是作者随便起的名字，和其本身的思想无关。

1 动态规划的思路

动态规划用于解决问题时需要明确的四个部分：

  • 1.1 确定状态
  1. 研究最优策略的最后一步。也就是问题的最后一步怎么做。
  2. 转化为子问题。知道了最后一步怎么做之后，那么最后一步的前一步是什么，总结之后就是子问题。

子问题和最后一步的问题相似的地方便是求解的重点。状态就是dp[i]---也就是动态规划数组中的i对应的元素的含义。通常dp[i]是我们要求的最优的目标，i是变化的量。

  • 1.2 转移方程

根据子问题的定义直接得到状态转移的方程。也就是dp[i]关于其他dp[j]的表达式。这里的表达式要么可以直接写出数学方程或者就是一个相关的描述。

  • 1.3 初始条件和边界情况

考虑问题的最开始的条件，以及问题的边界。

  • 1.4 计算顺序

利用之前的计算结果。利用先前计算好的结果求解当前需要计算的目标。

2 动态规划编程题

从简单到困难，依次来看看动态规划的编程题。

2.1 爬楼梯--Leetcode 70.爬楼梯

题目传送门

先来看题目和示例：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例：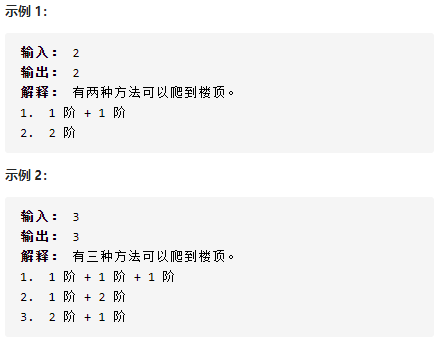

开始解题，你有什么想法吗？

我想到，这个题目的目的是爬到n阶楼梯上去，为了爬到 n 阶上面，根据题目的要求，那么我只能从 n-1 阶和 n-2。最后爬上去的情况考虑完了，那么再往前是怎么爬上来的呢？分析一下发现跟我们最后一步的情况一样的。所以，这个爬楼梯的问题就被分解掉了。对应第1节里面动态规划的思路，这部分是确定状态中要做的事情。子问题中一直在变化的是楼梯阶数，记为i。dp[i]就是我们要求的最优目标：爬到当前阶数i的方法总数。

从上面的分析我们能知道，所求目标dp[i]可以通过式子dp[i] = dp[i-1] + dp[i-2]，这个也就是转移方程（dp[i]关于其他dp[j]的表达式）。

该问题的初始条件和边界情况是第1阶和第2阶楼梯，它们的次数都是1。其余的位置初始化为0。

最后考虑计算顺序。因为后面的楼梯需要从前面的楼梯上去，所以需要自底向上进行计算。

Talk is cheap, show me the code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
	def climbStairs(self, n):
		dp = [0 for i in range(n+1)] # dp数组，初始化
		## 第1、2阶楼梯边界值
		dp[1] = 1 
		dp[2] = 2 
		## 高于2阶的楼梯的爬法计算
		for i in range(3, n+1):
			dp[i] = dp[i-1] + dp[i-2]
		return dp[n]
	## 仔细观察代码可以发现，其实很多数据用完一次后就没有再用到了，所以，改进上面代码的空间复杂度后的代码如下：
    def climbStairs(self, n: int) -> int:
        dp_i_2 = 1 ## dp[i-2]
        dp_i_1 = 2 ## dp[i-1]
        if n == 2:
            return dp_i_1
        if n == 1:
            return dp_i_2
        dp_i = 0 ## dp[i]
        for i in range(3, n+1):
            dp_i = dp_i_1 + dp_i_2
            tmp = dp_i_1
            dp_i_1 = dp_i
            dp_i_2 = tmp
        return dp_i

2.2 打家劫舍——LeetCode 198

python代码

1
2
3
4
5
6
7
8
9
def rob(nums):
	if len(nums) == 0:
		return 0
	dp = [0 for i in range(len(nums)+1)]
	dp[1] = nums[0]
	dp[2] = max(nums[0], nums[1])
	for i in range(3, len(nums)+1):
		dp[i] = max(dp[i-1], dp[i-2]+nums[i])
	return dp[len(nums)]