贪心算法

贪心算法的Introduction

贪心算法(贪心策略)是对采用了贪心技巧的方法的总称。贪心技巧就是在解决问题的每一步都采用最优的选择(每次都选最好的--所以就好贪心了，really greedy)。

贪心算法解决问题

假设有下面的一个场景。A、B、C、D代表一个城市不同的角落，现在你站在A角落想要尽快到达D。

从A出发可以走两条路，通往B或者C，利用贪心技巧：尽快到达终点的话，我现在这一步就要时间短的路径，所以选择B，到B之后直接到D。

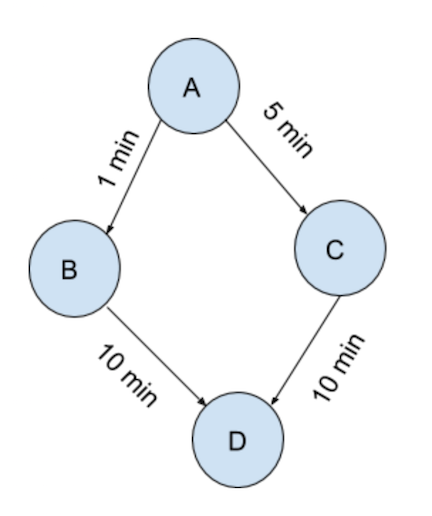
贪心算法存在的问题：假如有另外一个新的场景如下所示，利用贪心技巧的话，从A到D的路径便是：A -> B -> D，但是求出的路径(需要21min)并不是最快的，最快的是另外一条路径A -> C -> D (耗时15min)。

所以，由于没有考虑未来的情况，贪心算法有时并不会带来最优的解决方案，可能会带来一个低效的解决方案。一般来说，贪心算法往往比分治法(Divide and Conquer)、动态规划(Dynamic Programming)等效果差。

使用贪心算法时要注意分析贪心技巧是否对所有未来的步骤都奏效。

有关贪心算法的编程例子

问题陈述

最小操作数：从0开始，找到抵达目标值的最小操作数，每次操作只能包括下面的一种： * 加1 * 乘以2(加倍)

例子

  • 例1： 目标值为18，最小操作数为6，因为：
    • start = 0
    • step 1 ==> 0 + 1 = 1
    • step 2 ==> 1 * 2 = 2 # or 1 + 1 = 2
    • step 3 ==> 2 * 2 = 4
    • step 4 ==> 4 * 2 = 8
    • step 5 ==> 8 + 1 = 9
    • step 6 ==> 9 * 2 = 18
  • 例2： 目标值为69，最小操作数为9，因为：
    • start = 0
    • step 1 ==> 0 + 1 = 1
    • step 2 ==> 1 + 1 = 2
    • step 3 ==> 2 * 2 = 4
    • step 4 ==> 4 * 2 = 8
    • step 5 ==> 8 * 2 = 16
    • step 6 ==> 16 + 1 = 17
    • step 7 ==> 17 * 2 = 34
    • step 8 ==> 34 * 2 = 68
    • step 9 ==> 68 + 1 = 69

python实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def min_operations(target):
    """
    Return number of steps taken to reach a target number
    input:- target number an integer
    output:- number of steps an integer
    """
    num_steps = 0
    while target != 0:
        if target % 2 == 0:
            target = target // 2

        else:
            target = target - 1
        num_steps += 1
    return num_steps