机器学习中的优化方法

梯度下降法

梯度下降的目标是找到最优的权重 \(w\) 来最小化交叉熵损失函数。在下面的 最小化损失公式 中，损失方程 \(L_{CE}\) 的参数是权重---在机器学习中一般表示为 \(\theta\) (在逻辑回归里 \(\theta = w,b\))。所以，目标是找到最小化所有样本的平均损失函数的权重集合。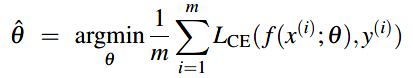

梯度下降法的思想与 \(\color{purple}{找一条下山最快的路}\)一致，也就是从当前位置最陡峭的方向往下走。\(\color{blue}{梯度}\) 用于描述函数曲线的陡峭程度，选择梯度最大也就是 \(\color{green}{最陡峭的方向走一定长度的步子}\)(步长也成为学习率--learning rate \(\eta\))，也就往最低的地方更近了一步，如下图所示(以单变量为例)。(最低的地方也就是损失函数的最低点或者极低点)。对于逻辑回归来说，交叉熵损失函数是凸函数，只有一个最低点，不会陷入到局部极小值，所以梯度下降从任一点开始都能找到最低点。

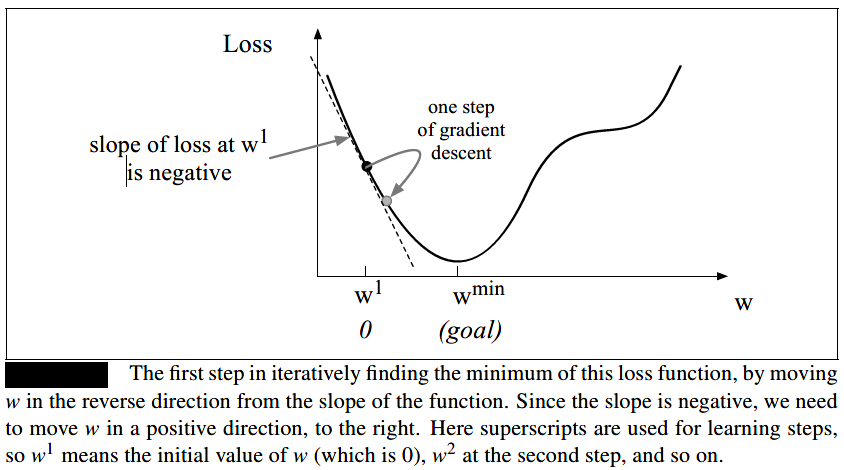
梯度下降对权重参数(如上图所示的单变量w)的做出的改变就是：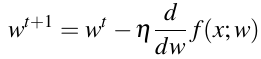

其中，\(\frac{d}{dw}f(x:w)\)就是图中的坡的方向。

现在将单变量扩展到多变量，因为我们不只是想知道往左往右(单变量的曲线)，还更想知道N维空间(对应组成 \(\theta\) 的N个参数)应该往哪个方向。此时的 \(\color{green}{梯度是一个向量}\) :它代表N维中的每个维的最陡峭方向。如果我们想象两维权重(一个是权重w，另一个是偏差b)，梯度就是包含两个正交项的向量，分别告诉我们在w维度和b维度上最陡峭的方向。下图中的红线可视化了红点处的梯度：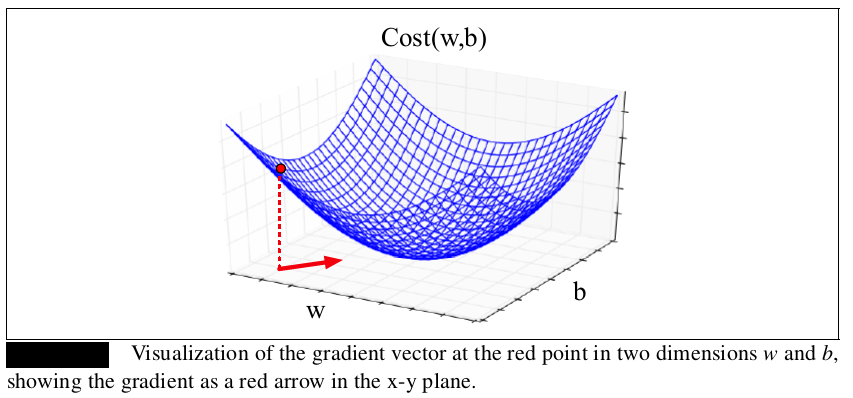

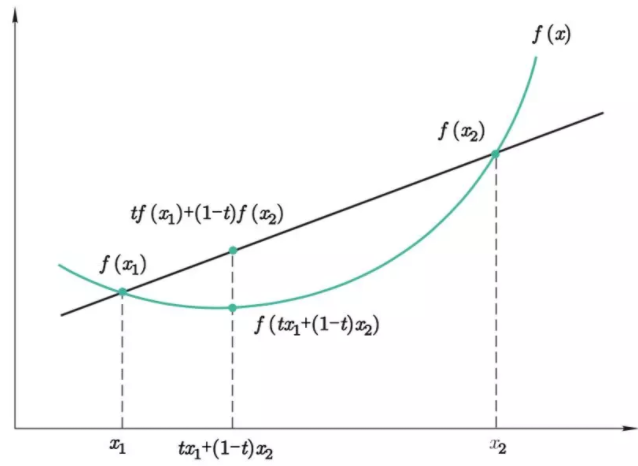
convex fucntion(凸函数，有的教材称其为凹函数)如下图中的f(x)曲线所示，其中t属于[0,1]。

多层神经网络的损失是非凸的，梯度下降会在训练的过程中陷入到局部极小值，从而找不到全局的最小值。

实际情况中，权重参数向量 \(\omega\)比较长，因为输入的特征向量x可能会比较长，特征向量x中的每个特征 \(x_i\)对应着一个权重\(w_i\)。对于权重向量\(w\)(加上偏差b)的每维\(w_i\)，梯度向量中都对应一项它的坡度(梯度) \(\frac{\partial}{\partial w_i}L\)，，如下公式所示：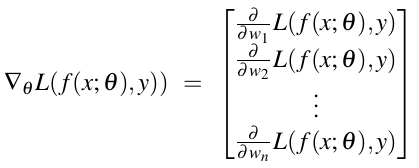

最后，更新权重参数向量的方式就是：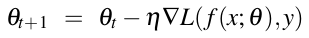

梯度下降法包含随机梯度下降算法。

随机梯度下降

学习率 \(\eta\) 是一个需要调整(我们自己手动设置)的超参数，太大就有可能跳过损失函数的最小值；太小就需要很长的时间走到损失函数的最小值。常见的做法就是从一个较大的值开始，然后慢慢地减小它，所以它是训练遍历次数k的函数，\(\eta_k\)代表第k次遍历的学习率。

随机梯度下降算法是一种online算法，它在每个训练样本后计算梯度来最小化损失函数。之所以叫随机是因为它每次随机选择单一样本进行学习，在每个单一样本上优化权重参数，来提高性能。随机梯度下降的算法伪码如下图所示：

小-批训练(Mini-batch training)

随机梯度下降一次随机选择单一样本，然后进行权重的更新，这就会带来权重跌宕起伏的改变，所以，最常见的方式是在训练样本的batches(批)上计算梯度。

对于batch training，它在整个数据集上计算梯度，通过观察所有的训练样本，batch training能够得出权重改变的最优的估计。缺点就是要花很多的时间处理训练集中的每个样本。折中的一个方式就是mini-batch training，它在m(可能是512或者1024)个样本一组的小批上训练，现在的损失方程就是m个样本中的每一个样本的损失之和的平均：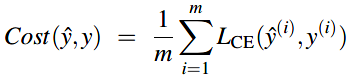

同时，mini-batch的梯度就是m个样本的梯度之和的平均值。