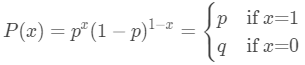概率分布

参考链接：链接1 链接2

每时每刻都有各种事情正在发生：骰子掷出、雨滴落下、巴士在路上。事件发生之前，我们只能讨论结果的可能性。概率分布描述了每种结果出现的概率。事件发生之后，特定的结果便确定了：掷出3点、今日降雨量是半英寸、巴士3分钟到站。有些时候，我们更关心概率分布，而不是最可能出现的单个结果。概率分布有各种形状，但是概率分布的概率之和恒等于1。

常见的概率分布包括均匀分布、伯努利分布、二项分布、多项分布、β分布、狄利克雷分布、高斯分布、KL散度。

均匀分布

均匀分布是定义在区间[a,b]上连续变量的简单概率分布，其概率密度函数 \(p(x)=\frac{1}{b-a}\) (b小于x小于a)如下图所示：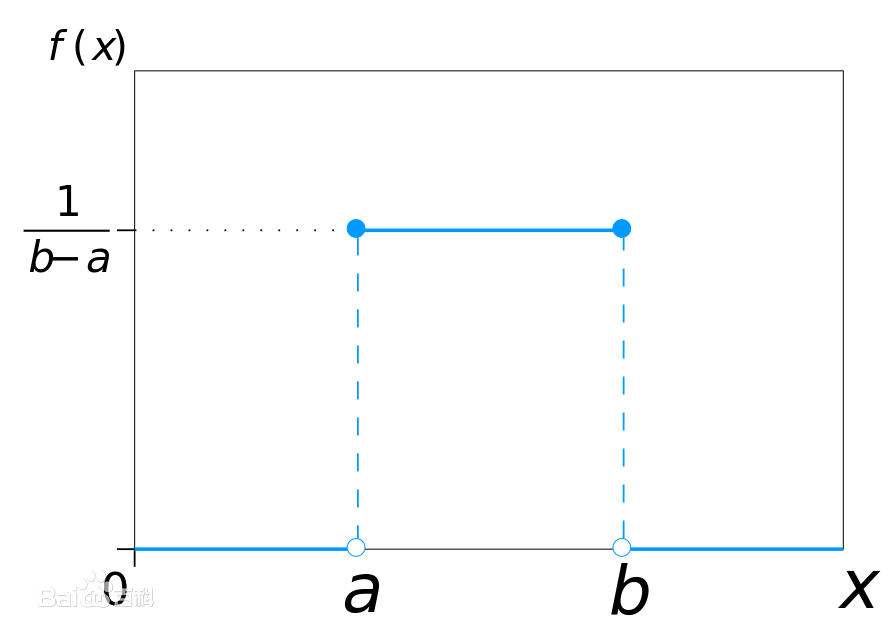

举例来说，掷骰子的结果可能是1到6之间的任意一个，得到任何一个结果的概率都一样(1/6)。

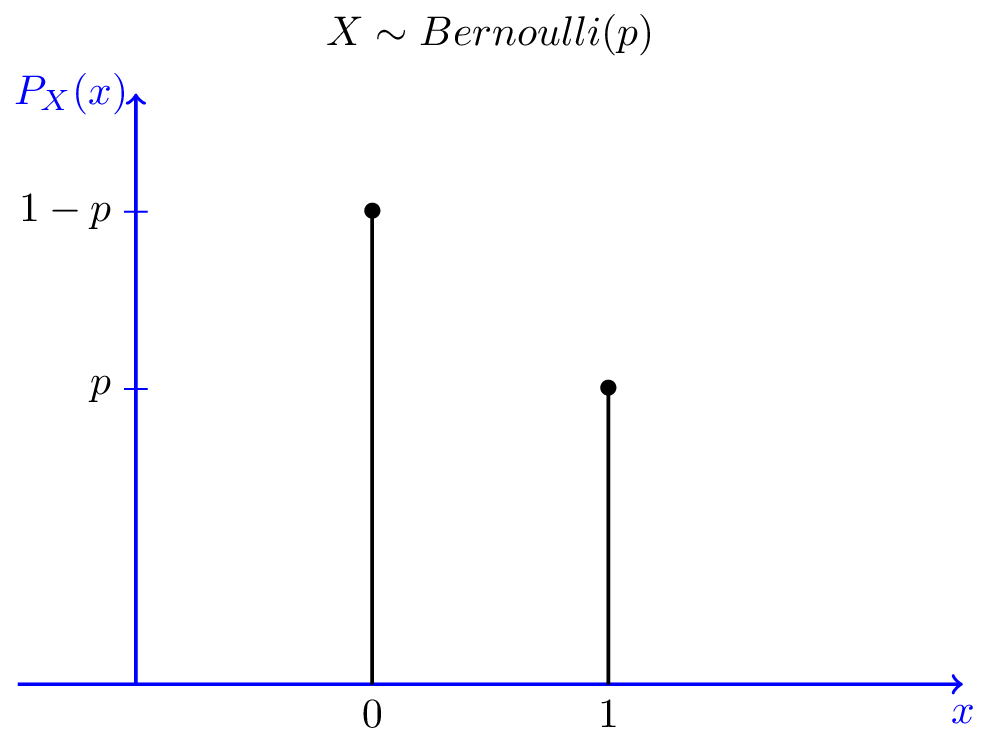
伯努利分布(Bernoulli)

抛掷一枚均匀硬币有两种结果：正面和反面(假设硬币不可能立起)。在扔硬币之前，我们相信有0.5的概率扔到正面，有0.5的概率扔到反面。这便是扔硬币的概率分布，也便是伯努利分布。

一个事件有两种离散结果：0或1(0、1分别表示两种结果)，其中1发生的概率为p，0发生的概率为1-p。上述便是伯努利分布。

很多概率分布都能自然地从伯努利分布导出，各种概率分布的相互关系图如下所示：

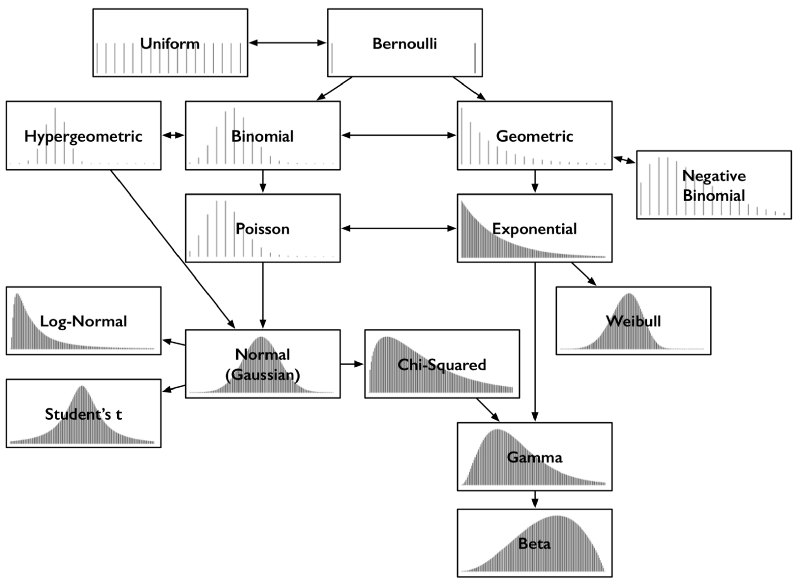
其中，上图中的每种概率分布都包含其相应的概率质量函数(离散变量)或概率密度函数(连续变量)，横轴为可能的数值结果的集合，纵轴为结果对应的概率。这上面，有些分布是离散的：每根线表示一种结果，线高表示该结果的概率，即概率质量函数本身就代表对应值的概率；有些分布是连续的：概率密度函数为连续的曲线，它本身不代表概率，\(\color{purple}{曲线下的面积表示概率}\)。概率质量函数的线高之和，概率密度函数的曲线下面积，恒为1。