二分查找

1 什么是二分查找

首先，我们来看 \(\color{purple}{线性查找(Linear Search)}\) 。对于一组无序的数字，想要从中查找某个数字的话就得从这组数字的头开始，依次往后比较，要么找到了该数字，要么找到了尾部都没有，那就是不存在这个数。上述过程就是线性查找，这组数字越长查找的性能就越差，时间复杂度为 O(n)。

是否有更好的查找方式呢？

二分查找就是。

如果我们拿到的是一组有序的数字，进行二分查找的方式是：首先比较 \(color{green}{中间位置}\) 的数字和目标是否相同，如果相同则结束查找，如果目标值小于中间位置的数字那么从左半边再找(查找步骤和上面一致)，如果目标值大于中间位置的数字那么从右半边再找(查找步骤和上面一致)。

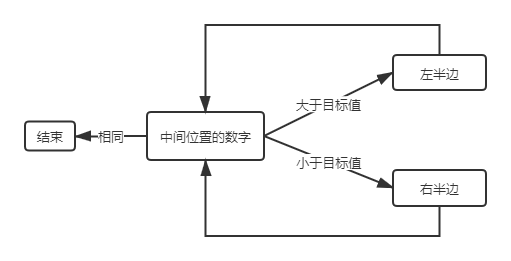
这个查找过程每次都直接缩减了一半的查找空间。现在来计算二分查找的时间效率：

\(color{purple}{最好的情况}\)： 第一次直接在中间位置找到。

\(color{purple}{最坏的情况}\)：找到了最后也没找到。那么查找的次数可以通过下面的方式计算：

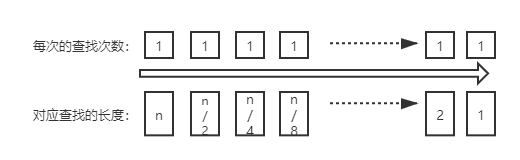
长度为n为一组数字，累积的查找次数就是上面的1的个数，1的个数正好是n每次除以2直到为1的次数：\(log_{2}n\) 。所以二分查找的时间效率为O(log(n))。

2 python实现二分查找

找到要查找的元素则返回其索引，否则返回-1。

2.1 迭代实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def binary_search(array, target):
    mid = len(array)//2
    low = 0
    high = len(array)
    while mid >= low or mid <= high:
        if array[mid] == target:
            print('find the target:', array[mid])
            return mid
        elif array[mid] < target:
            low = mid + 1
            mid = (low+high) // 2
        else:
            high = mid - 1
            mid = (low+high) // 2
    return -1

2.2 递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def binary_search(array, target, low, high):
    if low > high and low :
        return -1
    mid = (low+high) // 2
    if array[mid] == target:
        return mid
    elif array[mid] < target:
        low = mid + 1
        return binary_search(array, target, low, high)
    else:
        high = mid - 1
        return binary_search(array, target, low, high)
def binary_search_recursive(array, target):
    return binary_search(array, target, 0, len(array)-1)

3 基于二分查找的操作

3.1 Find First

二分查找能给出所要查找的元素的索引，如果要查找的元素在数组中出现多次呢？例如：[1, 3, 5, 7, 7, 7, 8, 11, 12]，要查找7的话，二分查找给出的索引是4，如果我们想要得到元素第一次出现的索引呢？

思想：二分查找得到元素的索引，然后一步步向前找相同元素，直到找到不相同的元素或者找到头，返回相应的索引。

给定二分查找：

1
2
3
4
5
6
7
8
9
10
def recursive_binary_search(target, source, left=0):
    if len(source) == 0: ## 元素不存在时返回None
        return None
    center = (len(source)-1) // 2
    if source[center] == target:
        return center + left
    elif source[center] < target:
        return recursive_binary_search(target, source[center+1:], left+center+1)
    else:
        return recursive_binary_search(target, source[:center], left)

Find First:

1
2
3
4
5
6
7
8
9
10
11
12
def find_first(target, source):
    index = recursive_binary_search(target, source, 0)
    if index == None:
        return None
    while source[index] == target:
        if index > 0:
            index -= 1
        elif index == 0:
            return index
        else:
            return None
    return index + 1

测试find_first： 

1
2
3
multiple = [1, 3, 5, 7, 7, 7, 8, 11, 12, 13, 14, 15]
print(find_first(7, multiple)) # Should return 3
print(find_first(9, multiple)) # Should return None
3 None

举一反三：如果想要找到元素最后一次出现的位置，只需要在上述代码中向后一步步查找即可。

Find Last:

1
2
3
4
5
6
7
8
9
10
def find_last(target, source):
    index = recursive_binary_search(target, source, 0)
    if index == None:
        return None
    while source[index] == target:
        if index < len(source) - 1:
            index += 1
        elif index == len(source) - 1:
            return index
    return index - 1

测试find_last: 

1
2
3
multiple = [1, 3, 5, 7, 7, 7, 8, 11, 12, 13, 14, 14]
print(find_last(7, multiple)) # Should return 5
print(find_last(14, multiple)) # Should return 11
5

11