二分类--逻辑回归分类器
1 逻辑回归简介
部分参考《Speech and Language Processing》。附上最新版链接电子版传送门
部分参考《统计学习方法》
逻辑回归是社会和自然科学最重要的分析方法之一。在自然语言处理中,逻辑回归是监督学习中分类方法的baseline,它和神经网络拥有十分亲近的关系,其实神经网络可以被看成是一系列的逻辑回归分类器堆叠起来的。
逻辑回归可以用于二分类(例如"positive"和"negative"),同样也可以用于多分类(多项式逻辑回归)。
深入了解逻辑回归之前,需要先明白的一些概念。
1 生成式和判别式分类器
关于生成式分类器(generative classifier)和判别式分类器(discriminative classifier):这是两种截然不同的机器学习模型框架。
举个例子:假设我们尝试分类猫和狗的图片。生成式模型的目标将会是理解狗长什么样子、猫长什么样子,你可以让模型"生成出"或者说成是画出一个狗。给定一张测试图片,系统会问是猫的模型更合适还是狗的模型更合适,然后选择更合适的那个作为它的标签。
判别式模型仅仅尝试学习区分类别(或许没有对其中的内容进行更多的学习)。所以可能训练集中所有的狗都有项圈,猫猫没有项圈,那么如果这个特征能很好地区别出不同的类别,模型就满意了。所以,如果你问模型它知道猫的什么内容的话,它会说猫没有项圈。
更正式地来说,无论什么样的机器学习模型都是为了能够对给定的输入预测相应的输出,一般形式为决策函数: \[ Y = f(X) \] 或者条件分布概率: \[ P(Y|X) \]
生成式模型首先从数据中学习联合概率分布 \(P(X,Y)\) ,然后再求出条件概率分布 \(P(Y|X)\) 作为预测模型: \[ P(Y|X) = \frac{P(X,Y)}{P(X)} \] 之所以称为生成方法是因为模型表示了给定输入\(X\)产生输出\(Y\)的生成关系。典型的生成模型包括:朴素贝叶斯和隐马尔科夫模型等等。
判别式模型由数据直接学习决策函数\(f(X)\)或者条件概率分布\(P(Y|X)\)作为预测的模型。判别式模型关心的是对于给定的输入\(X\),应该预测什么样的输出\(Y\)。典型的判别式模型包含:逻辑回归、k近邻、感知机、最大熵模型、支持向量机、条件随机场等等。
2 机器学习模型中的概率模型
首先,监督学习的模型可以是概率模型或者非概率模型,分别由条件概率分布 \(P(Y|X)\)、决策函数 \(Y = f(X)\) 表示。
假设训练集包含m条数据对 \((x_{(i)},y_{(i)})\),其中(i)代表训练集中单独的某条数据,那么概率模型包含下面几个组成成分:
- 输入的特征表示。对每条输入数据 \(x_{(i)}\),它的特征表示将会是一个特征向量 \([s_1, x_2, \cdots, x_n]\)。
- 分类方程,分类方程(或者称为预测方程)通过 \(p(y|x)\) 计算预测值 \(\hat{y}\) (也就是预测的类别)。分类方程有sigmoid和softmax等等。
- 目标方程,目标方程用于学习,通常包含在训练样本上最小化误差。目标方程包含交叉熵损失函数。
- 优化目标方程的算法。优化目标方程(损失函数)的算法包含随机梯度下降等等。
逻辑回归模型属于概率模型。逻辑回归模型有两个阶段:
训练阶段:利用随机梯度下降算法优化交叉熵损失来训练权重(w)和bias。
测试:给定一个测试用例 \(x\) ,计算 \(p(x|y)\),然后返回 \(y=1\) 和 \(y=0\)中更高概率的标签。
2 逻辑回归的分类函数:sigmoid
二分类逻辑回归的目标是训练一个可以对新的输入做出分类决策的分类器。sigmoid函数可以做出这种决策。
对于一个输入数据\(x\),我们可以将它表示为特征向量 \([x_1, x_2, x_3, \cdots, x_n]\),分类器的输出 \(y\) 可能是1或者是0。对于情感识别的任务,特征由词频表示,\(P(y=1|x)\)是输入数据\(x\)为positive的概率,\(P(y=0|x)\)是输入数据\(x\)为negative的概率。
逻辑回归通过从训练集中学习权重和偏差来处理上述任务。每个权重 \(w_i\)是一个实数值,它和输入数据的特征向量中的某维特征 \(x_i\) 相关,权重 \(w_i\) 代表了它对应的输入特征对分类决策的重要性,可能为正或者为负。所以,在情感识别任务中我们可能希望awesome一词拥有比较大的正值权重,abysmal一词有比较小的负值权重。偏差项(bias term)也是一个实数项,被加入到乘上权重的输入里。
在训练的过程中学习了权重后,为了在测试的时候做决策,分类器首先对输入数据的特征向量中的每个特征乘上它对应的权重 \(w_i\),然后把所有的乘积项加起来,再加上偏差项 \(b\),最后得到一个实数 \(z\) ( \(z\) 表示了它是某个类别的加权后的证据和): 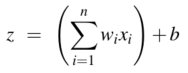 两个向量\(a\),\(b\)相乘可以表示为\(a \cdot b\),所以上式可以写为: \[
z = w \cdot x + b
\]
两个向量\(a\),\(b\)相乘可以表示为\(a \cdot b\),所以上式可以写为: \[
z = w \cdot x + b
\]
为了以概率的形式表现,将 \(z\) 通过sigmoid方程使其输出为0到1之间的数值。sigmoid函数图像看起来像s,它也被称为逻辑方程,所以逻辑回归模型的名字由此确定。Sigmoid函数表示式为: 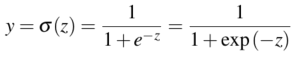
sigmoid函数图像为: 
sigmoid函数的有很多优点。它以实数值作为输入,输出[0,1]区间的数值,正好可以作为概率。从图像中可以看出,在输入靠近0的时候图像接近线性,然后两边的图像逐渐变平,它将异常值(过小或者过大)压缩到0或者1。sigmoid函数是可微分的,适合学习过程。
所以,利用sigmoid函数可以将加权后的特征和映射到[0,1]区间。为了让它符合概率分布,我们要确保两个类别的概率 \(p(y=1)\)、\(p(y=0)\) 之和为1,方式为:(同时下述公式即为 \(\color{purple}{逻辑回归模型}\)) 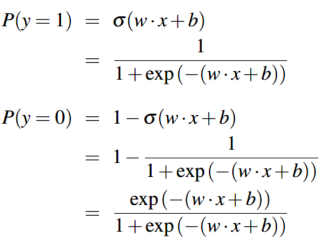
线性函数\(w \cdot x+b\)的值越接近正无穷,概率值\(P(Y=1|x)\)越接近于1;线性函数\(w \cdot x+b\)的值越接近负无穷,概率值\(P(Y=1|x)\)越接近于0。这样的模型就是逻辑回归模型。
现在我们有了一个给定输入 \(x\) 计算概率 \(P(y=1|x)\)的算法。那我们该如何决策?方法就是:对于一个测试用例 \(x\) ,如果概率 \(P(y=1|x)\)大于0.5,那么它就属于1类,如果小于0.5就属于0类,即决策边界为:
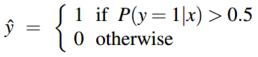
3 逻辑回归的学习过程
逻辑回归为有监督学习,通过减小预测值和实际值之间的误差来调整模型参数。
学习需要两大组件。第一个就是衡量预测值和实际值之间差距的metric(度量),通常使用的度量(metric)是两者之间的distance(距离)而非相似度,distance(距离)被称为损失方程或者代价方程。经常使用在逻辑回归和神经网络中的损失方程为交叉熵损失见博客。第二个就是为了最小化损失函数的优化方程,去迭代更新权重参数。常用的方法为梯度下降(包含随机梯度下降)等等。
交叉熵损失函数
逻辑回归所用的损失函数为交叉熵损失函数 \(L_{CE}\): 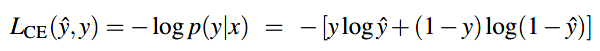
由逻辑回归所用分类函数/激活函数为sigmoid知:\(\hat{y}=\sigma(w \cdot x + b)\),代入得: 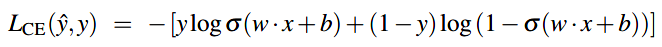
梯度下降
关于梯度下降参考我的另一博客传送门
为了更新参数 \(\theta\),需要知道它在损失函数中的梯度,已知逻辑回归的损失函数为交叉熵损失函数: 
那么该损失函数的偏微分项就是: 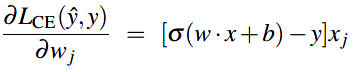 (分析公式可知上面的梯度是估计值和真实值之差乘以相应的输入值)
(分析公式可知上面的梯度是估计值和真实值之差乘以相应的输入值)
多分类--逻辑回归分类器
多项式逻辑回归
对于有些任务,它是有多个类别需要区分的,这个时候就开始利用 \(\color{green}{多项式逻辑回归(multinomial logistic regression)}\),也叫做softmax regression,或者更历史一点的叫最大熵分类器(maxent classifier)。在多项式逻辑回归中,目标 \(y\) 是变化范围为多个类别(多于两个)的变量。在分类的时候,我们需要知道\(y\)在每个可能的类别中的概率 \(p(y=c|x)\)。
多项式逻辑回归分类器使用sigmoid的一般形式:softmax方程去计算分类的概率 \(p(y=c|x)\)。softmax方程将k个任意的值组成的向量 \(z=[z_1, z_2, \cdots, z_k]\) 映射到一个概率分布上。对于k维的向量 \(z\)的某个元素 \(z_i\),softmax定义为:

对于向量 \(z=[z_1, z_2, \cdots, z_k]\) ,softmax的形式就为:
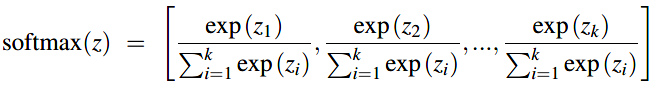
与sigmoid类似,替换\(z = w \cdot x + b\),与sigmoid不同的是:需要分开k个类别中的每个类别对应的权重向量和偏差向量。: 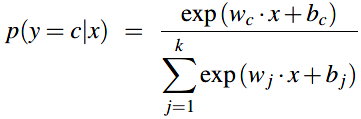
多项式逻辑回归的学习过程
上面知道了二分类逻辑回归的交叉熵方程: 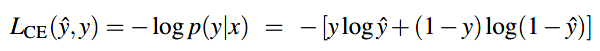
多项式逻辑方程的损失函数把上面式子中的两项一般化到K项: 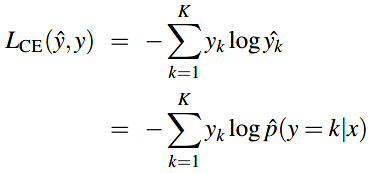
实际的y是onehot向量,即只有样本x对应的类别处为1,其余类别为0。 
其中,\(\Bbb1 \{y=k\}\)是指示函数,只有 \(y=k\) 时为1,其余为0。
所以实际上该交叉熵损失方程就只是正确类别的估计值的负对数: 