正则化
为什么需要正则化?
在训练的过程中学习权重的时候存在一个问题就是模型会完美匹配训练数据。如果一个特征十分适合预测结果,它就会被赋上一个很大的权重。特征的权重会努力去完美拟合训练样本的细节,这时的完美其实就是过完美,它会学到偶然发生的噪声。这样的结果就是,模型在训练集上的效果很好,但是在测试集上的效果比较差,也就是 \(\color{purple}{过拟合}\)。一个好的模型应该有能力从训练集到测试集(unseen test set)进行泛化(generalize),也就是对没有见过的样本也能比较好地进行分类。
为了避免过拟合问题,模型可以加入正则化。
什么是正则化?
正则化项(regularization term) \(R(\theta)\) 可以加到目标方程中来防止过拟合。例如如下最大化正确分类的对数概率公式中(假设是mini-batch训练,m个样本一个batch,公式里去掉了1/m这个系数,因为不影响目标): 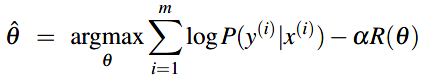
新的正则化项 \(R(\theta)\) 用于惩罚大的权重。所以对于一个能对训练数据很好分类的权重集合A(但它使用很多值很大的权重做到的)和一个对训练数据很好分类的权重集合B(使用的权重值更小),正则化对A的惩罚会更大。有两种常见的计算正则化项 \(R(\theta)\) 的方式:L1正则化与L2正则化。
\(\color{green}{L2正则化}\)是权重值的二次方程,称为L2是因为它使用L2 norm(范数)的(平方的)权重值,L2 norm(范数):\(\parallel \theta \parallel_{2}\) 和 \(\theta\) 离原点的欧式距离一致。如果 \(\theta\) 包含n个权重,\(R(\theta)\) 为: 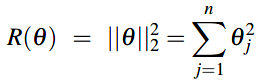
目标方程增加L2正则化项后: 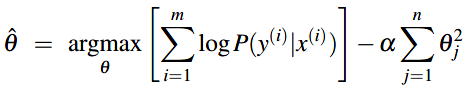
\(\color{green}{L1正则化}\)是权重值的线性方程,称为L1是因为使用L1 norm(范数):权重值的绝对值之和,它和曼哈顿距离一致。 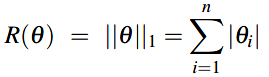
目标方程增加L1正则化项后: 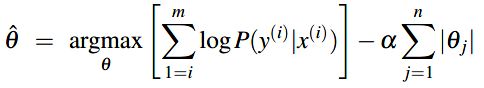
在训练过程中使用L2正则化更容易,因为它的导数比较简单。L2正则化倾向于得到有很多小权重值的权重向量,L1正则化更倾向于得到稀疏向量---有一些较大值的权重和很多值为0的权重,所以L1正则化得到的特征更少。