简单的机器翻译

1 任务描述

通过词向量和向量空间模型，将英文词翻译为法语词。

2 任务的数据

来自维基百科上的英文单词对应的词向量，以及法语单词对应的词向量。

但是全部的词及其词向量太大，所以只选择的部分数据。

2.1 数据的预处理

这部分是要生成单词和其词向量的字典。已经生成好的字典文件在这，直接利用en_embeddings.p和fr_embeddings.p文件即可。

获取数据字典：

import pickle

en_embeddings_subset = pickle.load(open("en_embeddings.p", "rb"))
fr_embeddings_subset = pickle.load(open("fr_embeddings.p", "rb"))

### 2.2 数据的格式

上一步得到的数据为：

• en_embeddings_subset:键是英语词汇，值是300维的词向量。

  'the': array([ 0.08007812, 0.10498047, 0.04980469, 0.0534668 , -0.06738281, ....

• fr_embeddings_subset:键是法语词汇，值是300维的词向量。

  'la': array([-6.18250e-03, -9.43867e-04, -8.82648e-03, 3.24623e-02,...

接着我们创建英文单词与法语单词的字典，即英文单词:法语单词。(用到的文件路径和上面的字典文件一样)

import pandas as pd

def get_dict(file_name):
	my_file = pd.read_csv(file_name, delimiter=' ')

	etof = {}

	for i in range(len(my_file)):
		en = my_file.iloc[i][0]
		fr = my_file.iloc[i][1]
		etof[en] = fr

	return etof

en_fr_train = get_dict('en_fr.train.txt')
print('The length of the English to French training dictionary is', len(en_fr_train))
en_fr_test = get_dict('en_fr.test.txt')
print('The length of the English to French test dictionary is', len(en_fr_train))

创建好的英文单词:法语单词词典如下所示：

{'the': 'la',
'and': 'et',
'was': 'était',
'for': 'pour',

## 3 简单的机器翻译--利用线性变换进行单词翻译

3.1 生成输入和输出矩阵

这里将上面的数据生成矩阵形式，即利用英文单词:法语单词和英文单词:词向量以及法语单词：词向量生成英文词向量:法语词向量的矩阵。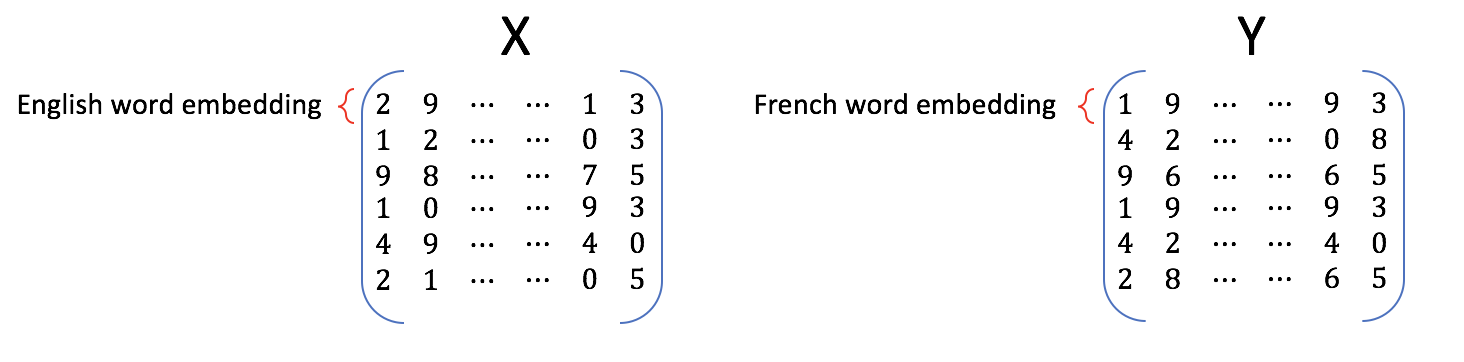

import numpy as np

def get_matrices(en_fr, french_vecs, english_vecs):
	    """
    Input:
        en_fr: English to French dictionary
        french_vecs: French words to their corresponding word embeddings.
        english_vecs: English words to their corresponding word embeddings.
    Output: 
        X: a matrix where the columns are the English embeddings.
        Y: a matrix where the columns correspong to the French embeddings.
    """
    X_l = list()
    Y_l = list()

    english_set = english_vecs.keys()
    french_set = french_vecs.keys()

    for en_word, fr_word in en_fr.items():
    	if fr_word in french_set and en_word in english_set:
    		en_vec = english_vecs[en_word]
    		fr_vec = french_vecs[fr_word]

    		X_l.append(en_vec)
    		Y_l.append(fr_vec)

    X = np.vstack(X_l)
    Y = np.vstack(Y_l)
    return X, Y

X_train, Y_train = get_matrices(en_fr_train, fr_embeddings_subset, en_embeddings_subset)

3.2 线性变换以及计算损失方程

给定输入矩阵X(英语单词的词向量组成)和输出矩阵Y(法语单词的词向量组成)，生成变换矩阵R。算法核心可以描述为： \[ XR = Y \]

将上述思想描述维最小化问题即为： \[ \arg \min _{\mathbf{R}}\| \mathbf{X R} - \mathbf{Y}\|_{F}\tag{1} \]

其中\(XR - Y\)的2-范数： \[ \| \mathbf{XR} - \mathbf{Y}\|_ {F} \] 就是矩阵所有值各自平方然后求和再开根号。

为了方便进行求导寻找最小值误差，通常计算的是 \[ \frac{1}{m} \| \mathbf{X R} - \mathbf{Y} \|_ {F}^{2} \]

其中，m是样本的数量，除以m是因为我们更关注每个词向量的平均损失而不是整个训练集的总损失，让我们忽略掉训练集的大小。计算2-范数的平常是因为它比根号求导更简单。

所以，最终的损失方程为：

\[ L(X, Y, R)=\frac{1}{m}\sum_{i=1}^{m} \sum_{j=1}^{n}\left( a_{i j} \right)^{2} \] 其中，\(a_{i j}\)是 \(\mathbf{XR}-\mathbf{Y}\) 矩阵第i行第j列的值。

def compute_loss(X, Y, R):
	m = X.shape[0]
	diff = np.dot(X, R) - Y
	diff_squared = diff**2
	sum_diff_squared = np.sum(diff_squared)
	loss = sum_diff_squared/m
	return loss

3.3 计算损失方程的梯度

关于变换矩阵R计算损失方程的梯度： \[ \frac{d}{dR}𝐿(𝑋,𝑌,𝑅)=\frac{d}{dR}\Big(\frac{1}{m}\| X R -Y\|_ {F}^{2}\Big) = \frac{2}{m}X^{T} (X R - Y) \]

def compute_gradient(X, Y, R):
	m = X.shape[0]
	gradient = np.dot(X.T, np.dot(X, R)-Y)*(2/m)

	return gradient

3.4 使用梯度下降法寻找最优线性变换矩阵R

梯度下降法是用于寻找函数最优值的迭代算法。

通常我们迭代一定的训练次数来终止而不是设置一个训练损失的界限。(我们最应该关注的是验证集损失的下降validation loss或者验证集准确度的上升，如果验证机准确度开始下降了的话说明已经过拟合了。)

我们用上面计算得到的梯度\(g\)，再设置一定的学习率(步长)\(\alpha\)来更新变换方程： \[ R_{\text{new}}= R_{\text{old}}-\alpha g \]

def update(X, Y, train_steps=100, learning_rate=0.003):
	np.random.seed(129)

	R = np.random.rand(X.shape[1], X.shape[1])

	for i in range(train_steps):
		if i%25 == 0:
			print("loss at iteration {} is {:.4f}".format(i, compute_loss(X, Y, R)))
		gradient = compute_gradient(X, Y, R)

		R -= learning_rate*gradient

	return R

计算我们翻译用到的转换矩阵：

R_train = update(X_train, Y_train, train_steps=400, learning_rate=0.8)

## 4 测试翻译结果

给定测试案例\(e\)，计算它翻译后的法语词向量：\(eR\)，然后在法语词向量矩阵集合中寻找最相近的词向量，也就是找到了翻译后的法语词。

那么直接在法语词向量矩阵中一行一行计算相似度求最小值的话是很慢的，为了寻找高效的解决办法，在这里利用KNN(k最近邻)算法，也就是在其周围最近的一个聚类里计算即可(不用全部都去计算)。

首先，我们利用余弦相似度来描述词向量的相似度：

def cosine_similarity(A, B):
	cos = 0
	dot = np.dot(A, B)
	norm_a = np.linalg.norm(A)
	norm_b = np.linalg.norm(B)

	return dot/(norm_a*norm_b)

接着我们来计算knn聚类后得到的近似：

def knn(v, candidates, k=1):
	"""
    Input:
      - v, the vector you are going find the nearest neighbor for
      - candidates: a set of vectors where we will find the neighbors
      - k: top k nearest neighbors to find
    Output:
      - k_idx: the indices of the top k closest vectors in sorted form
    """
    similarity_l = []

    for row in candidates:
    	cos_similarity = cosine_similarity(v, row)
    	similarity_l.append(cos_similarity)

    sorted_ids = np.argsort(similarity_l)

    k_idx = sorted_ids[-k:] ##默认相似值从小到大，所以从后面大的开始

    return k_idx

### 测试准确度

测试翻译的准确度。

def test_vocabulary(X, Y, R):
	pred = np.dot(X, R)
	num_correct = 0

	for i in range(len(pred)):
		pred_idx = knn(pred[i], Y) ## 默认k=1
		if pred_idx == i:
			num_correct += 1

	accuracy = num_correct/len(pred)
	return accuracy

计算翻译准确度：

X_val, Y_val = get_matrices(en_fr_test, fr_embeddings_subset, en_embeddings_subset)
acc = test_vocabulary(X_val, Y_val, R_train)  # 需要几分钟
print(f"accuracy on test set is {acc:.3f}")