蒸汽量预测

案例来源：天池大赛——工业蒸汽量预测传送门。

1 赛题背景

火力发电的基本原理是：燃料在燃烧时加热水生成蒸汽，蒸汽压力推动汽轮机旋转，然后汽轮机带动发电机旋转，产生电能。在这一系列的能量转化中，影响发电效率的核心是锅炉的燃烧效率，即燃料燃烧加热水产生高温高压蒸汽。

锅炉的燃烧效率的影响因素很多，包括锅炉的可调参数，如燃烧给量，一二次风，引风，返料风，给水水量；以及锅炉的工况，比如锅炉床温、床压，炉膛温度、压力，过热器的温度等。

2 赛题描述

经脱敏后的锅炉传感器采集数据(采集频率是分钟级别)，根据锅炉的工况预测产生的蒸汽量。

3 数据说明

数据分成训练数据（train.txt）和测试数据（test.txt），其中字段”V0”-“V37”，这38个字段是作为特征变量，”target”作为目标变量。我们需要利用训练数据训练出模型，预测测试数据的目标变量，排名结果依据预测结果的MSE（mean square error）—— 评价指标。

4 案例分析和解决方案

4.1 导入包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import warnings
warings.filterwarnings('ignore')
import matplotlib.pyplot as plt
import seaborn as sns

## 模型相关的包
import pandas as pd
import numpy as np
from scipy import stats
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV, RepeatedKFold, cross_val_score, cross_val_predict, KFold
from sklearn.metrics import make_scorner, mean_squared_error
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
from sklearn.svm import Linear_SVR, SVR
from sklearn.neighbors import KNeighborsRegression
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, AdaBoostRegressor
from xgboost import XGBRegressor
from sklearn.preprocessing import PolynomialFeatures, MinMaxScaler, StandardScaler

4.2 加载数据

1
2
data_train = pd.readcsv('train.txt', sep='\t')
data_test = pd.readcsv('test.txt', sep='\t')
1
2
3
4
5
6
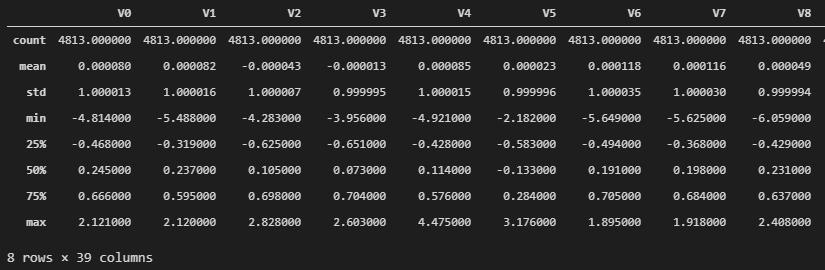
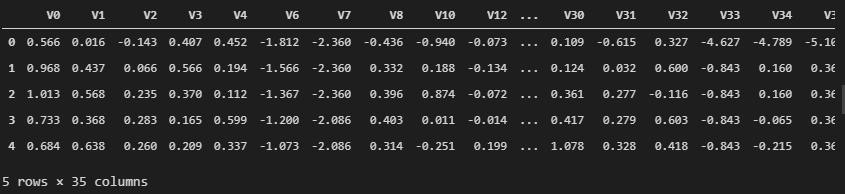
## 合并训练数据和测试数据
data_train['oringin'] = 'train'
data_test['oringin'] = 'test'
data_all = pd.concat([data_train, data_test], axis=0, ignore_index=True)

data_all.head() ## 展示前五条数据

1
data_all.describe() ## 数据描述

4.3 探索数据分布

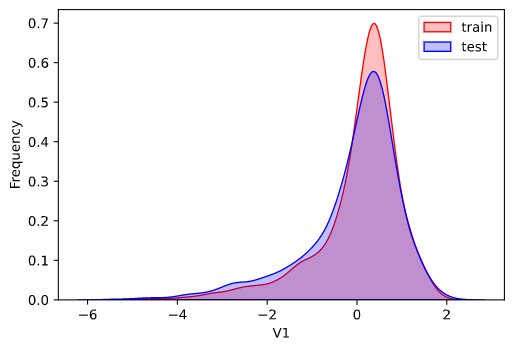
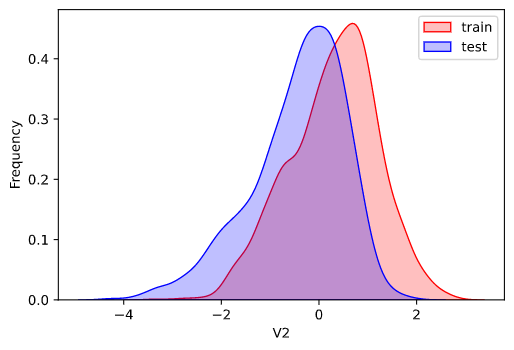
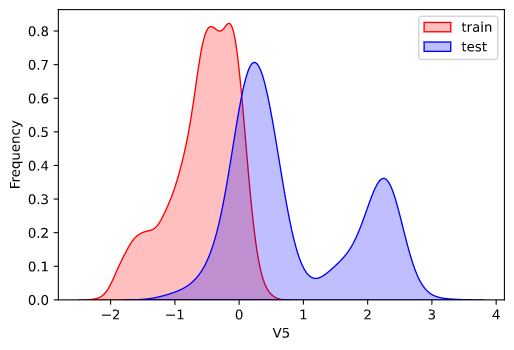
因为数据为传感器数据，即连续变量，所以使用核密度估计图(kdeplot)进行数据的初步分析(EDA:Exploratory data analysis)。

seaborn中的kdeplot函数参数、作用以及使用方法可以参考官方教程：传送门

1
2
3
4
5
6
7
8
for column in data_all.column[0: -2]: ## 遍历特征列
	#核密度估计(kernel density estimation)是在概率论中用来估计未知的密度函数，属于非参数检验方法之一。通过核密度估计图可以比较直观的看出数据样本本身的分布特征。
	g = sns.kdeplot(data_all[column][(data_all['oringin'] == 'train')], color='Red', shade=True)
	g = sns.kdeplot(data_all[column][(data_all['oringin'] == 'test')], ax=g, color='Blue', shade=True)
	g.set_xlabel(column)
	g.set_ylabel('Frequency')
	g = g.legend(['train', 'test'])
	plt.show()

部分输出：

从上面的各特征概率分布函数曲线可以看出特征"V5","V9","V11","V17","V22"中训练集数据分布和测试集数据分布不均，所以我们删除这些特征数据。

1
2
3
4
5
6
7
8
9
10
# for column in ['V5', 'V9', 'V11', 'V17', 'V22']:
# 	g = sns.kdeplot(data_all[column][(data_all['oringin'] == 'train')], color='Red', shade=True)
# 	g = sns.kdeplot(data_all[column][(data_all['oringin'] == 'test')], ax=g, color='Blue', shade=True)
# 	g.set_xlabel(column)
# 	g.set_ylabel('Frequency')
# 	g = g.legend(['train', 'test'])
# 	plt.show()

data_all.drop(['V5', 'V9', 'V11', 'V17', 'V22'], axis=1, inplace=True)
data_all.head()

输出：

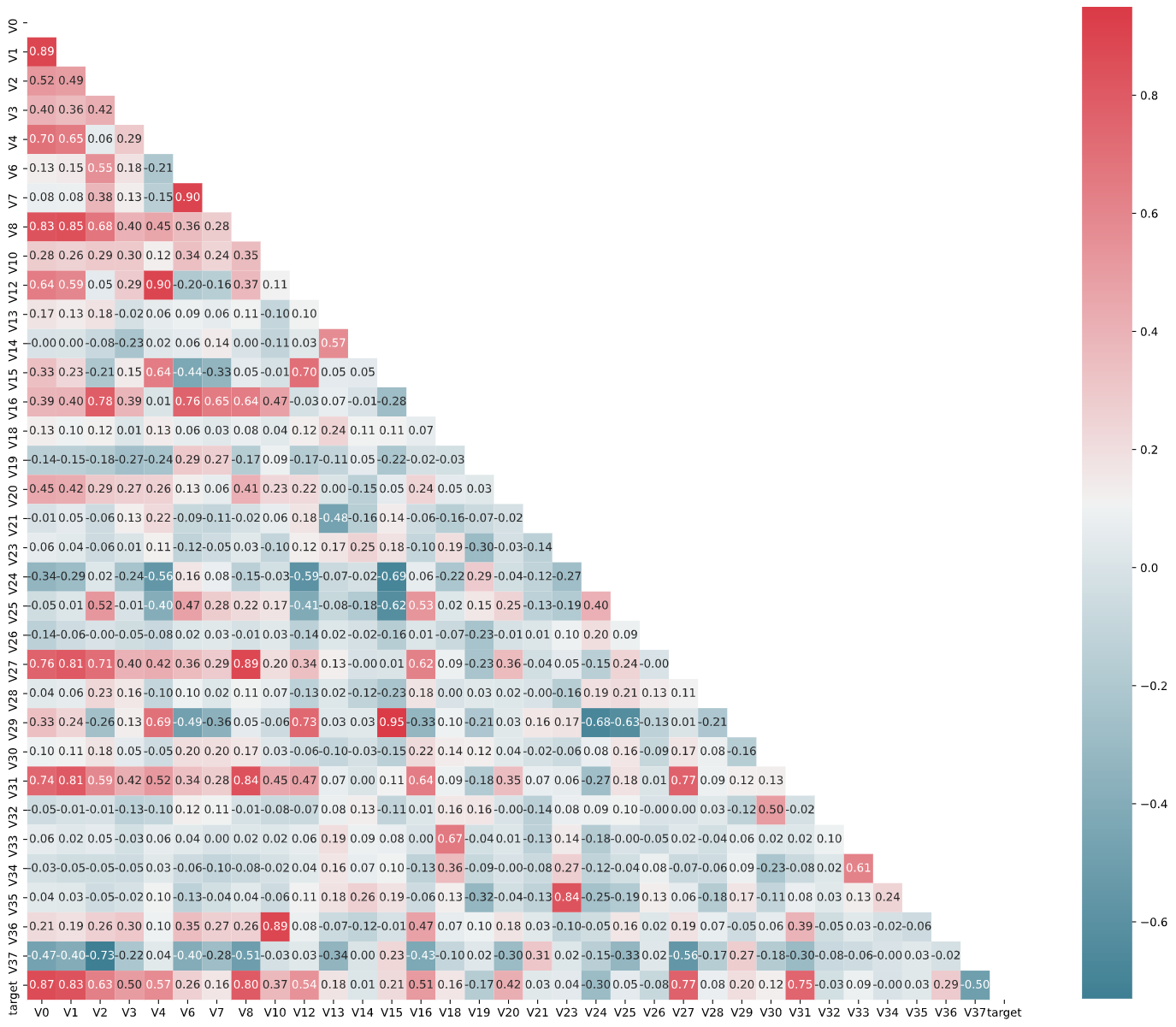
接下来进行查看特征之间的相关性(相关程度)。

1
2
3
4
5
6
7
8
9
data_train1 = data_all[data_all['oringin'] == 'train'].drop('oringin', axis=1) ## axis=1：删除列
plt.figure(figsize=(20, 16)) ## 指定绘图对象宽度和高度
col = data_train1.columns.tolist() ## 列表头
mcorr = data_train1[col].corr(method='spearman') ## 相关系数矩阵，即给出了任意两个变量之间的相关关系
mask = np.zores_like(mcorr, dtype=np.bool) ## 构造与mcorr同维数矩阵，为bool型。
mask[np.triu_indices_from(mask)] = True ## 对角线右侧为true
cmap = sns.diverging_palette(220, 10, as_cmap=True) ## 返回matplotlib colormap对象，调色板
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')  # 热力图（看两两相似度）
plt.show()

输出：

接下来继续进行降维操作。将和目标变量——蒸气值(target)相关性的绝对值小于阈值的特征进行删除。

1
2
3
4
5
threshold = 0.1
corr_matrix = data_train1.corr().abs()
print('corr_matrix:', corr_matrix)
drop_col = corr_matrix[corr_matrix['target'] < threshold].index
data_all.drop(drop_col, axis=1, inplace=True)

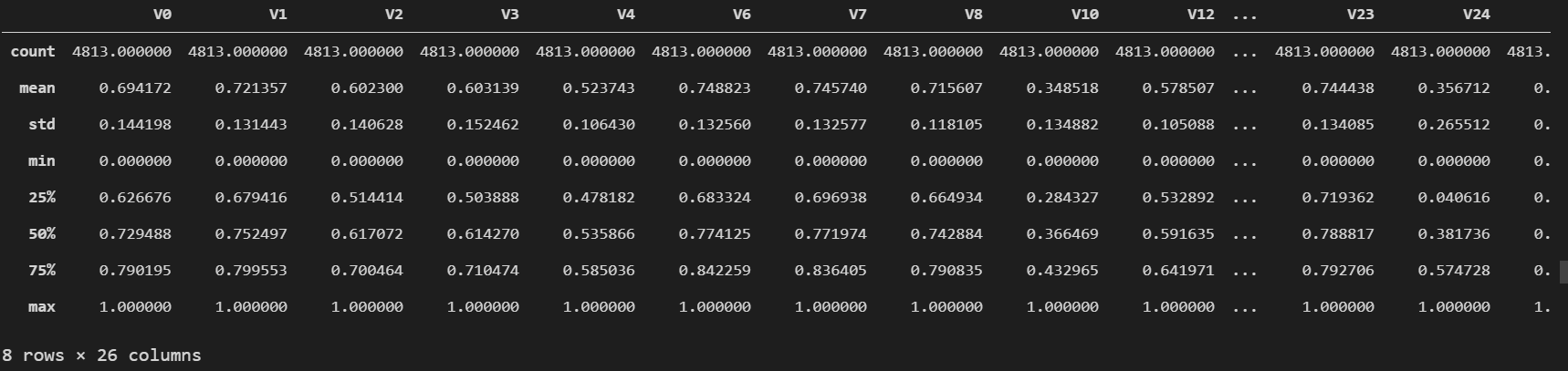
进行归一化操作：

1
2
3
4
5
6
7
8
9
cols_numeric = list(data_all.columns)
cols_numeric.remove('oringin')

def scale_minmax(col):
	return (col-col.min()) / (col.max()-col.min())

scale_cols = [col for col in cols_numeric if col != 'target']
data_all[scale_cols] = data_all[scale_cols].apply(scale_minmax, axis=0)
data_all[scale_cols].describe()

4.4 特征工程

进行Box-Cox变换前，首先来看一下该变换对数据分布的影响。

关于Box-Cox变换可以参考：(传送门)[https://wenku.baidu.com/view/96140c8376a20029bd642de3.html]

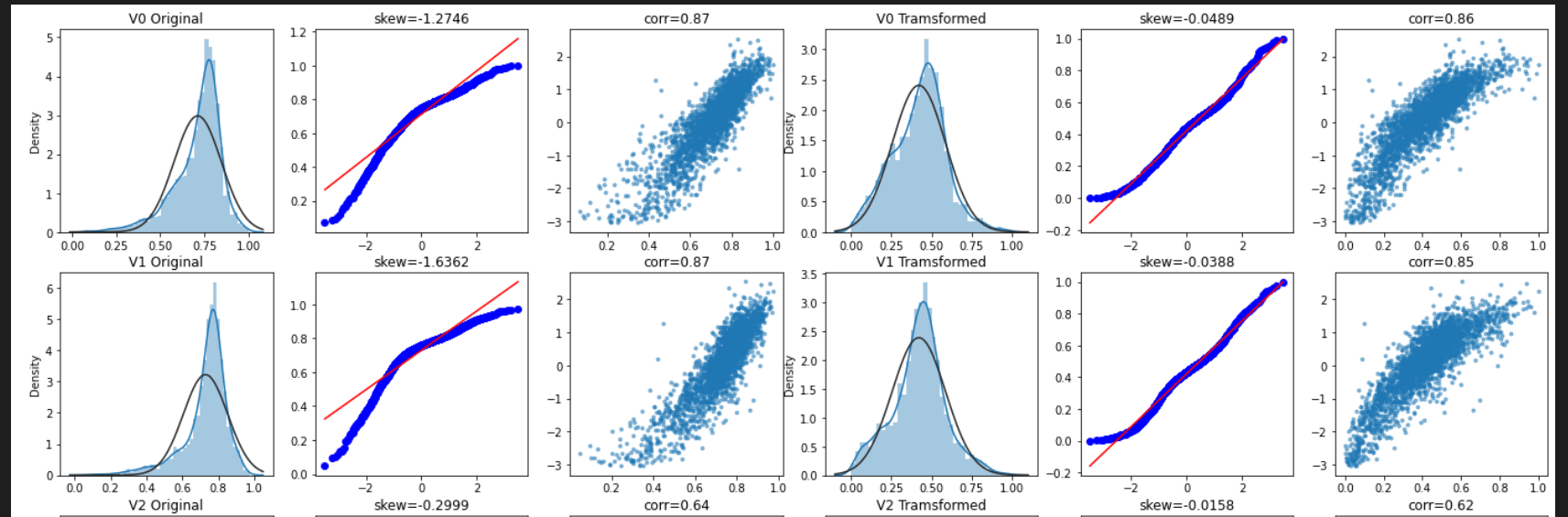
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
fcols = 6
frows = len(cols_numeric) - 1
plt.figure(figsize=(4*fcols, 4*frows))
i = 0

for var in cols_numeric:
	if var != 'target':
		dat = data_all[[var, 'target']].dropna()

		i += 1
		plt.subplot(frows, fcols, i)
		sns.distplot(dat[var], fit=stats.norm)
		plt.title(var+' Original')
        plt.xlabel('')
        
        i+=1
        plt.subplot(frows,fcols,i)
        _=stats.probplot(dat[var], plot=plt)
        plt.title('skew='+'{:.4f}'.format(stats.skew(dat[var])))
        plt.xlabel('')
        plt.ylabel('')
        
        i+=1
        plt.subplot(frows,fcols,i)
        plt.plot(dat[var], dat['target'],'.',alpha=0.5)
        plt.title('corr='+'{:.2f}'.format(np.corrcoef(dat[var], dat['target'])[0][1]))
 
        i+=1
        plt.subplot(frows,fcols,i)
        trans_var, lambda_var = stats.boxcox(dat[var].dropna()+1)
        trans_var = scale_minmax(trans_var)      
        sns.distplot(trans_var , fit=stats.norm)
        plt.title(var+' Tramsformed')
        plt.xlabel('')
        
        i+=1
        plt.subplot(frows,fcols,i)
        _=stats.probplot(trans_var, plot=plt)
        plt.title('skew='+'{:.4f}'.format(stats.skew(trans_var)))
        plt.xlabel('')
        plt.ylabel('')
        
        i+=1
        plt.subplot(frows,fcols,i)
        plt.plot(trans_var, dat['target'],'.',alpha=0.5)
        plt.title('corr='+'{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))
plt.show()

部分输出截图：

在进行Box-Cox变换之后，可以一定程度上减小不可观测的误差和预测变量的相关性。

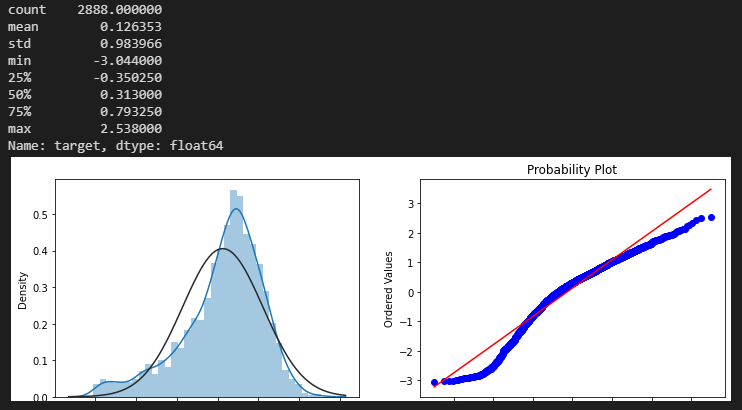
1
2
3
4
5
6
7
8
9
10
11
# 进行Box-Cox变换
cols_transform = data_all.columns[0:-2]
for col in cols_transform:
	data_all.loc[:, col], _ = stats.boxcox(data_all.loc[:, col]+1)
print(data_all.target.describe())
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1) ## 子图一共1行2列，该图(紧接着的下面的图)是第1个
sns.distplot(data_all.target.dropna(), fit=stats.norm)
plt.subplot(1, 2, 2)
_ = stats.probplot(data_all.target.dropna(), plot=plt)
plt.show()

输出：

可对target目标值使用对数变换，提升正态性。

1
2
3
4
5
6
7
8
sp = data_train.target
data_train.target1 = np.power(1.5, sp)

plt.figure(figsize(12, 4))
plt.subplot(1, 2, 1)
sns.distplot(data_train.target1.dropna(), fit=stats.norm)
plt.subplot(1, 2, 2)
_ = stats.probplot(data_train.target1.dropna(), plot=plt)

输出：

4.5 模型构建以及集成学习

  • a. 构建训练集和测试集
1
2
3
4
5
6
7
8
9
10
11
12
def get_training_data():
	df_train = data_all[data_all['oringin']=='train']
	df_train['label'] = data_train.target1

	y = df_train.target
	X = df_train.drop(['oringin', 'target', 'label'], axis=1)
	X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.3, random_state=100)
	return X_train, X_valid, y_train, y_valid

def get_test_data():
	df_test = data_all[data_all['oringin'] == 'test'].reset_index(drop=True)
	return df_test.drop(['oringin', 'target'], axis=1)

————

  • b. RMSE、MSE的评价函数

RMSE:Root Mean Squard Error，均方根误差，是MSE(均方误差)开根号得到的值。

1
2
3
4
5
6
7
8
9
def rmse(y_true, y_pred):
	diff = y_pred - y_true
	sum_sq = sum(diff**2)
	n = len(y_pred)
	return np.sqrt(sum_sq/n)

def mse(y_true, y_pred):
	return mean_squared_error(y_true, y_pred)

————

  • c. 寻找离群值并删除
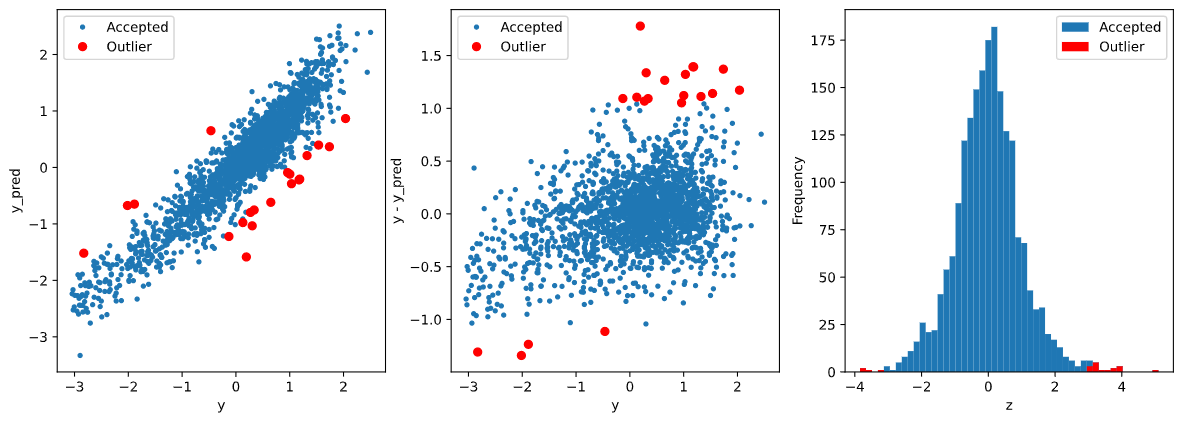
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
def find_outliers(model, X, y, sigma=3):

	model.fit(X, y)
	y_pred = pd.Series(model.predict(X), index=y.index)

	resid = y - y_pred
	mean_resid = resid.mean()
	std_resid = resid.std()

	z = (resid - mean_resid)/std_resid
	outliers = z[abs(z)>sigma].index

	print('R2=', model.score(X, y))
	print('rmse=', rmse(y, y_pred))
	print('mse=', mse(y, y_pred))
	print('---------------------------------------')

	print('mean of residual:', mean_resid)
	print('std of residual:'. std_resid)
	print('---------------------------------------')

	print(len(outliers), 'outliers:')
	print(outliers.tolist())

	plt.figure(figsize(15, 5))
	ax_131 = plt.subplot(1, 3, 1)
	plt.plot(y, y_pred, '.')
	plt.plot(y.loc[outliers], y_pred.loc[outliers], 'ro')
	plt.legend(['Accepted', 'Outliers'])
	plt.xlabel('y')
	plt.ylabel('y_pred')

	ax_132=plt.subplot(1,3,2)
    plt.plot(y,y-y_pred,'.')
    plt.plot(y.loc[outliers],y.loc[outliers]-y_pred.loc[outliers],'ro')
    plt.legend(['Accepted','Outlier'])
    plt.xlabel('y')
    plt.ylabel('y - y_pred')

    ax_133=plt.subplot(1,3,3)
    z.plot.hist(bins=50,ax=ax_133)
    z.loc[outliers].plot.hist(color='r',bins=50,ax=ax_133)
    plt.legend(['Accepted','Outlier'])
    plt.xlabel('z')

    return outliers
1
2
3
4
5
6
7
8
X_train, X_valid, y_train, y_valid = get_training_data()
test = get_test_data()

outliers = find_outliers(Ridge(), X_train, y_train)
X_outliers = X_train.loc[outliers]
y_outliers = y_train.loc[outliers]
X_t = X_train.drop(outliers)
y_t = y_train.drop(outliers)

输出： 

1
2
3
4
5
6
7
8
9
R2= 0.8767013861653619
rmse= 0.3489631754674053
mse= 0.12177529783229514
---------------------------------------
mean of residuals: -6.172422515926897e-16
std of residuals: 0.3490495418034555
---------------------------------------
20 outliers:
[2655, 2159, 1164, 2863, 1145, 2697, 2528, 2645, 691, 1874, 2647, 884, 2696, 2668, 1310, 1458, 2769, 2002, 2669, 1972]

  • d. 进行模型的训练
1
2
3
4
def get_training_data_omitOutliers():
	y = y_t.copy()
	X = X_t.copy()
	return X, y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
def train_model(model, param_grid=[], X=[], y=[], splits=5, repeats=5):

	if len(y) == 0:
		X, y = get_training_data_omitOutliers()

	## 交叉验证
	rkfold = RepeatedKFold(n_splits=splits, n_repeats=repeats)

	## 网格搜索最佳参数
	if len(param_grid) > 0:
		gsearch = GridSearchCV(model, param_grid, cv=rkfold, scoring='neg_mean_squared_error', verbose=1, return_train_score=True)

		## 训练
		gsearch.fit(X, y)

		## 最好的模型
		model = gsearch.best_estimator_
		best_idx gsearch.best_index_

		## 获取交叉验证评价指标
		grid_results = pd.DataFrame(gsearch.cv_results_)
		cv_mean = abs(grid_results.loc[best_idx, 'mean_test_score'])
		cv_std = grid_results.loc[best_idx, 'std_test_score']
	else: ## 没有网格搜索
		grid_results = []
		cv_results = cross_val_score(model, X, y, scoring='neg_mean_squared_error', cv=rkfold)
		cv_mean = abs(np.mean(cv_results))
		cv_std = np.std(cv_results)

	## 合并数据
	cv_score = pd.Series({'mean':cv_mean, 'std':cv_std})

	## 预测
	y_pred = model.predict(X)

	## 模型性能的统计数据
	# 模型性能的统计数据        
    print('----------------------')
    print(model)
    print('----------------------')
    print('score=',model.score(X,y))
    print('rmse=',rmse(y, y_pred))
    print('mse=',mse(y, y_pred))
    print('cross_val: mean=',cv_mean,', std=',cv_std)

    ## 残差分析与可视化
    y_pred = pd.Series(y_pred, index=y.index)
    resid = y - y_pred
    mean_resid = resid.mean()
    std_resid = resid.std()
    z = (resid - mean_resid)/std_resid
    n_outliers = sum(abs(z)>3)
    outliers = z[abs(z)>3].index

    return model, cv_score, grid_results
1
2
3
4
5
## 定义训练变量存储数据
opt_models = dict()
score_models = pd.DataFrame(columns=['mean', 'std'])
splits = 5
repeats = 5
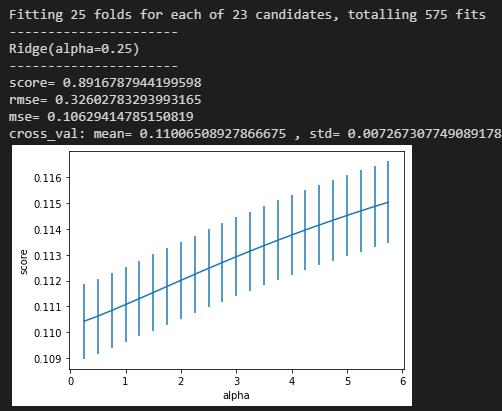
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
model = 'Ridge' ## 可替换
opt_models[model] = Ridge() ## 可替换
alph_range = np.arange(0.25, 6, 0.25)
param_grid = {'alpha':alph_range}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, splits=splits, repeats=repeats)

cv_score.name = model
score_models = score_models.append(cv_score)

plt.figure()
plt.errorbar(alph_range, abs(grid_results['mean_test_score']), abs(grid_results['std_test_score'])/np.sqrt(splits*repeats))
plt.xlabel('alpha')
plt.ylabel('score')
plt.show()

输出： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
## 预测函数
def model_predict(test_data, test_y=[]):
	i = 0
	y_predict_total = np.zeros((test_data.shape[0],))
	for model in opt_models.keys():
		if model != 'LinearSVR' and model != 'KNeighbors':
			y_predict = opt_models[model].predict(test_data)
			y_predict_total += y_predict
		if len(test_y) > 0:
			print('{}_mse:'.format(model), mean_squared_error(y_predict, test_y))
	y_predict_mean = np.round(y_predict_total/i, 6)
	if len(test_y) > 0:
		print("mean_mse:",mean_squared_error(y_predict_mean,test_y))
	else:
		y_predict_mean=pd.Series(y_predict_mean)
        return y_predict_mean

————

  • e. 模型的预测和结果的保存
1
2
y_ = model_predict(test)
y_.to_csv('predict.txt', header=None, index=False)