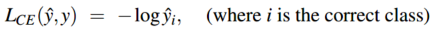机器学习中的损失函数
损失函数用于确定预测值 \(\hat{y}\) 和实际值 \(y\) 之间的距离:
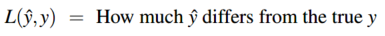
交叉熵损失
交叉熵损失函数利用的是负对数似然损失(negative log likelihood loss)。假设现在的输入为 \(x\),我们想要学习能够最大化正确标签的概率\(p(y|x)\) 的权重参数。对于二分类来说,仅有两个离散的输出(0和1),这是个伯努利分布(Bernouli distribution),我们可以将输入 \(x\) 对应的分类器得出的 \(p(y|x)\) 表示为:
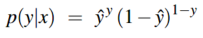
上式就是指如果 \(y=1\) ,\(p(y|x)=\hat{y}\),如果 \(y=0\),\(p(y|x)=1-\hat{y}\)。
现在对上面的式子两边同时取对数: 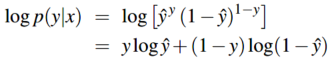
取对数能够让计算更加简单,同时最大化正确分类的概率也会最大化概率的对数。上面的式子就是应该最大化的对数概率,为了将它变为损失函数(一般最小化),直接在式子前面加负号就得到交叉熵损失 \(L_{CE}\): 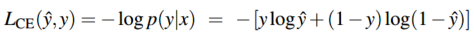
其中 \(\hat{y}=\sigma(w \cdot x + b)\)。最小化交叉熵损失就能得到最大化得正确分类的概率p(y|x)。为什么最小化这个负对数概率就能得到我们想要的呢?因为一个好的分类器会给正确的输出(y=1或者y=0)给概率赋值1,给错误的输出赋值概率为0。概率的负对数是一个很好的误差衡量方式,因为它的值变化是从0(1的负对数,也就是说分类正确,误差为0)到正无穷(0的负对数,此时是无穷大的损失)
对于多分类任务来说,\(y\)是一个关于 \(C\) 类别的向量,代表输出的概率分布,这时交叉熵损失为: 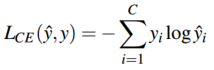
如果是一个硬分类任务,就是说仅仅有一个类别是正确的,如果对于当前的输入,它正确的类别是 \(i\) ,那么输出向量 \(y\) 中仅有 \(y_i=1\),其余为0,这也就是one-hot向量。那么上面的多分类交叉熵损失就变成: