逻辑回归分类器实现情感识别

任务描述

识别推文中的情感是积极的还是消极的。

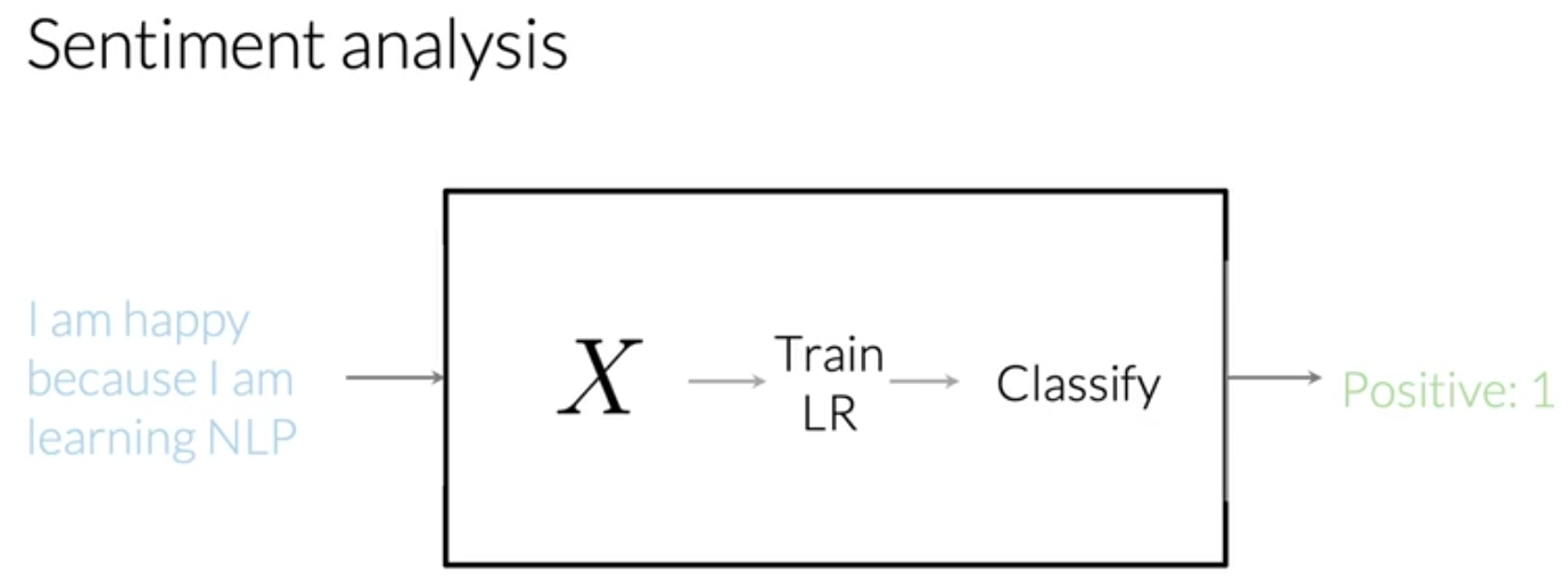
给定一个推文： I am happy because I am learning NLP

现在，任务目标就是判断上面的推文是积极的情感(positive sentiment)还是消极的情感(nagetive sentiment)。

给定一个训练集，训练集中包含推文和其对应的标签(label)，标签取值为1(代表positive)和0(代表negative)。

任务数据集

NLTK语料库中的tweet数据集。

目录

  • 一、数据预处理
  • 二、逻辑回归分类器
  • 三、特征提取
  • 四、训练模型
  • 五、测试所写逻辑回归分类器

一、数据预处理

1.1 用向量表示文本(represent a text as a vector)

为了用向量来表示文本，首先需要创建一个词汇表(vocabulary)，根据词汇表把文本(text)编码为数组(数组里面是数字)。

在该任务中，遍历数据集所有的推文，将所有的推文用到的全部词汇整理为词汇表(不含重复的词语)。

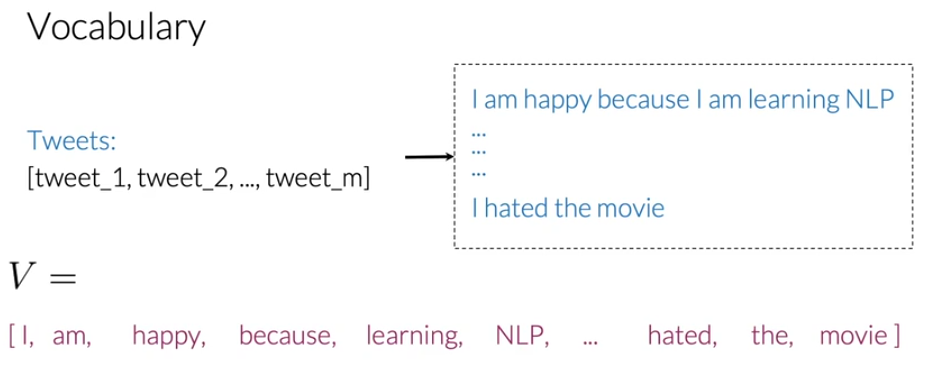
根据上述词汇表，进行推文的特征提取(feature extraction)：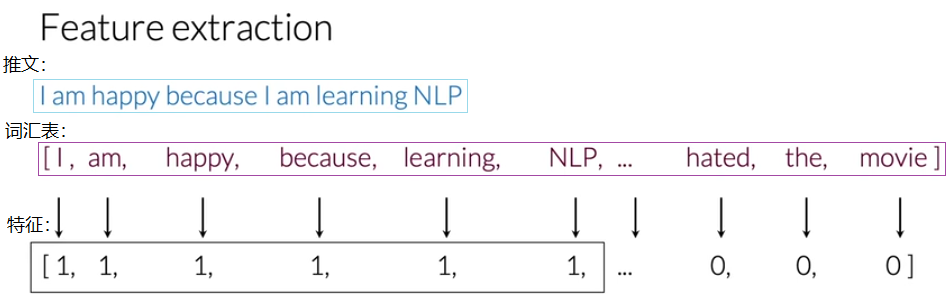

其中，1代表对应词汇表处的单词出现，0代表词汇没有出现。I am happy because I am learning NLP就被表示为[1,1,1,1,1,1,0,0,0,...,0,0,0]，特征长度为V(词汇表的大小)，其中一共有 6 个1(就算I和am出现两次，但是只用1和0来表示词(word)是否出现，而不看出现的次数)和 V-6 个0。这种表示方式拥有相对较少的非零值，大部分都是0，所以被称为稀疏表示(sparse representation)。

对于上述表示方式，逻辑回归分类器需要学习n个参数(n为词汇表的大小)。如果任务涉及的词汇表十分长，就会导致训练时间很长，同样参数越多的话也会让预测的时间变很长。

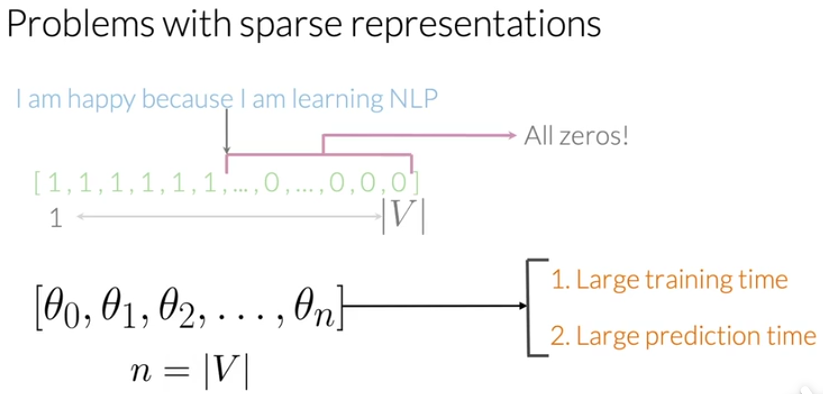
解决方式之一就是利用词(word)在不同类(标签)中出现的次数(count)——frequency作为逻辑回归分类器的特征。举例如下：假设语料库(数据集)为4条推文的集合，而且得出了它对应的词汇表：

对于数据集中标签为positive的数据(推文)，计算其出现的词汇的positive frequency：

对于数据集中标签为negative的数据(推文)，计算其中出现的词汇的negative frequency：

最终得不同类别得词频为：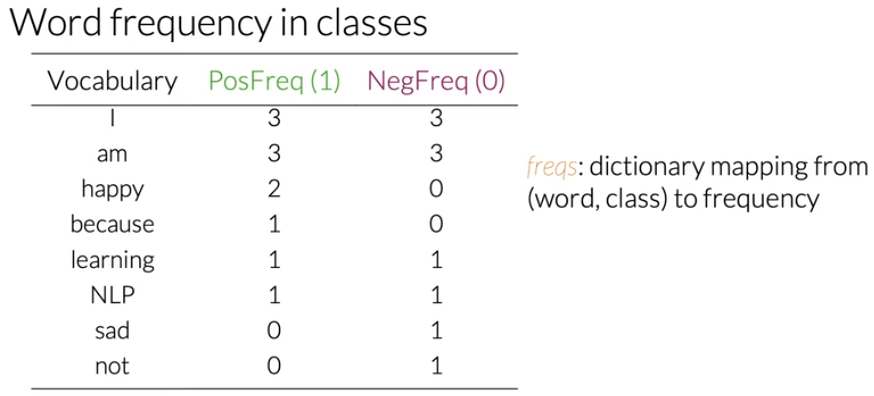

上述词频表的数据结构为字典(dictionary)freqs，将(word, class)映射到了frequency。

现在利用频率字典提取特征。

将任意一条推文(数据) \(X_m\) 表示为一个3维向量，而不是V维向量，如下：

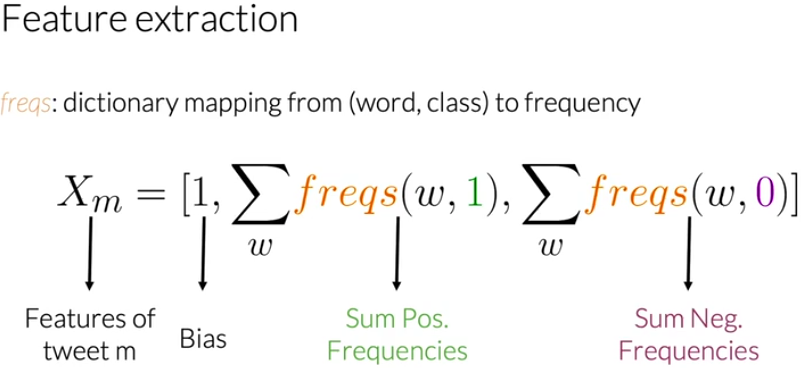
其中，特征向量的第一维是Bias(偏差)，第二维是所有词语的positive frequency，第三维是所有词语的negative frequency。举个例子来说： 对于 I am sad, I am not learning NLP ，所有word的positive frequency之和为8： 所有word的negative frequency之和为：

所以，对于推文 I am sad, I am not learning NLP ，它的特征向量为 \(X_m\)为： \[ X_m = [1, 8, 11] \]

1.2 预处理文本

上面学习了如何根据文本构造逻辑回归的特征，那么这里开始看如何对文本进行预处理。

1 stop words 和 punctuation(标点)

在提取特征前，需要去除stop words，因为stop words通常是没有意义的词语，例如下图中的stop words表，这只是其中很小的一部分(对当前例子来说完全足够)。有时候文本中的punctuation(标点)对任务没有影响，这时就可以根据punctuation表来去除标点。

去除stop words
去除标点符号

去除stop words和punctuation后的文本还有可能包含句柄或url，对于情感识别任务，句柄或url没有影响，所以可以去除。

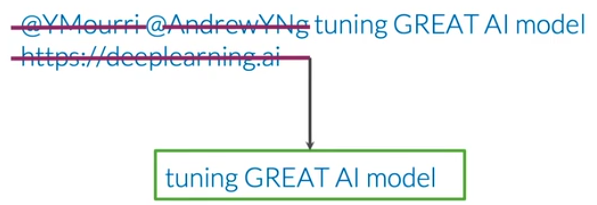
如果某任务中标点符号具有重要信息或者价值，就不用去除标点符号。

2 Stemming(词干提取) 和 lowercasing(小写化)

词干提取(stemming)可以减少统计同一词语的不同形式，词汇量能够大大减少。小写化所有词能够统一词语。

经过上述处理最后得到的推文为:[tun, great, ai, model]。

1.3 代码

导入包

1
2
3
4
5
import nltk
from os import getcwd
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

下载NLTK里的推文数据集和stopwords

1
2
# nltk.download('twitter_samples')
# nltk.download('stopwords')

准备数据

twitter_samples包含5000条积极推文和5000条消极推文。(其实有关于tweet有三个数据集）

1
from nltk.corpus import twitter_samples 
1
2
3
4
5
6
7
8
9
10
11
12
13
all_positive_tweets = twitter_samples.strings('positive_tweets.json')
all_negative_tweets = twitter_samples.strings('negative_tweets.json')
## 80%的用于训练，20%用于测试
train_pos = all_positive_tweets[:4000]
test_pos = all_positive_tweets[4000:]

train_neg = all_negative_tweets[:4000]
test_neg = all_negative_tweets[4000:]

train_x = train_pos + train_neg
test_x = test_pos + test_neg
train_y = np.append(np.ones((len(train_pos), 1)), np.zeros((len(train_neg), 1)), axis=0)
test_y = np.append(np.ones((len(test_pos), 1)), np.zeros((len(test_neg), 1)), axis=0)
1
2
3
4
5
print('training data')
print(train_x[0])
print(train_y[0])
print("train_y.shape = " + str(train_y.shape))
print("test_y.shape = " + str(test_y.shape))
training data
#FollowFriday @France_Inte @PKuchly57 @Milipol_Paris for being top engaged members in my community this week :)
[1.]
train_y.shape = (8000, 1)
test_y.shape = (2000, 1)

预处理数据并创建词频字典

  1. 预处理推文
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.tokenize import TweetTokenizer
import re
import string

## 预处理推文的函数
def process_tweet(tweet):
    stemmer=PorterStemmer()
    stopwords_english=stopwords.words('english')
    
    # remove stock market tickers like $GE
    tweet = re.sub(r'\$\w*', '', tweet)
    # remove old style retweet text "RT"
    tweet = re.sub(r'^RT[\s]+', '', tweet)
    # remove hyperlinks
    tweet = re.sub(r'https?:\/\/.*[\r\n]*', '', tweet)
    # remove hashtags
    # only removing the hash # sign from the word
    tweet = re.sub(r'#', '', tweet)
    
    tokenizer=TweetTokenizer(preserve_case=False,strip_handles=True,
                             reduce_len=True)
    
    tweet_tokens=tokenizer.tokenize(tweet)
    
    tweets_clean=[]
    # remove stopwords
    # remove punctuation
    for word in tweet_tokens:
        if word not in stopwords_english and\
            word not in string.punctuation:
            stem_word=stemmer.stem(word)
            tweets_clean.append(stem_word)
    return tweets_clean
  1. 创建词频字典
1
2
3
4
5
6
7
8
9
10
11
12
## 创建词频字典的函数
def build_freqs(tweets,ys):
    yslist = np.squeeze(ys).tolist()
    freqs = {}
    for y,tweet in zip(yslist,tweets):
        for word in process_tweet(tweet):
            pair=(word,y)
            if pair in freqs:
                freqs[pair]+=1
            else:
                freqs[pair]=1
    return freqs
1
freqs = build_freqs(train_x, train_y)
1
print('len(freqs)', len(freqs))
len(freqs) 11340

二、逻辑回归分类器

关于逻辑回归分类器参考我的另一篇博客：传送门

分类函数:sigmoid

  • sigmoid方程:

\[ h(z) = \frac{1}{1+\exp^{-z}} \tag{1}\] \[z = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + ... \theta_N x_N\]

1
2
def sigmoid(z):
    return 1/(1+np.exp(-z))

损失函数与梯度下降

  • 损失函数(全部训练样本的平均损失): \[J(\theta) = -\frac{1}{m} \sum_{i=1}^m y^{(i)}\log (h(z(\theta)^{(i)})) + (1-y^{(i)})\log (1-h(z(\theta)^{(i)}))\tag{5} \] 其中，m是训练样本的数量。
  • 梯度下降 关于梯度下降法，见博客 损失方程\(J\)关于权重参数中的一个\(\theta_j\)的梯度为: \[\nabla_{\theta_j}J(\theta) = \frac{1}{m} \sum_{i=1}^m(h^{(i)}-y^{(i)})x_j \tag{5}\] 其中，i是样本数的索引，j是权重参数的索引。 一般地有: \[\nabla J(\theta) = \frac{1}{m} \times \left( \mathbf{x}^T \cdot \left( \mathbf{h-y} \right) \right)\] 那么，参数更新的公式即为: \[\mathbf{\theta} = \mathbf{\theta} - \frac{\alpha}{m} \times \left( \mathbf{x}^T \cdot \left( \mathbf{h-y} \right) \right)\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
## 梯度更新函数
def gradient(x, y, theta, alpha, num_iters):
    m = x.shape[0]
    
    for i in range(num_iters):
        z = np.dot(x, theta)
        h = sigmoid(z)
        J = -1./m * (np.dot(y.transpose(), np.log(h)) + np.dot((1-y).transpose(),np.log(1-h)))
        theta = theta-(alpha/m)*np.dot(x.transpose(), (h-y))
    print("J1", J)
    J = float(J)
#     print("J2", J)
    ## 返回损失和更新后的梯度
    return J, theta
1
2
3
4
5
6
7
8
9
10
11
12
# Check the function
# Construct a synthetic test case using numpy PRNG functions
np.random.seed(1)
# X input is 10 x 3 with ones for the bias terms
tmp_X = np.append(np.ones((10, 1)), np.random.rand(10, 2) * 2000, axis=1)
# Y Labels are 10 x 1
tmp_Y = (np.random.rand(10, 1) > 0.35).astype(float)

# Apply gradient descent
tmp_J, tmp_theta = gradient(tmp_X, tmp_Y, np.zeros((3, 1)), 1e-8, 700)
print(f"The cost after training is {tmp_J:.8f}.")
print(f"The resulting vector of weights is {[round(t, 8) for t in np.squeeze(tmp_theta)]}")
J1 [[0.6709497]]
The cost after training is 0.67094970.
The resulting vector of weights is [4.1e-07, 0.00035658, 7.309e-05]

三、特征提取

这里提取推文中的两个特征:

  • 一个特征是积极词的数量(标签为积极的推文中出现的词的词频)；
  • 另外一个特征是消极词的数量(标签为消极的推文中出现的词的词频)。
1
2
3
4
5
6
7
8
9
10
11
12
13
## 特征提取函数
def extract_features(tweet, freqs):
    word_l = process_tweet(tweet)
    x = np.zeros((1, 3))

    x[0,0] = 1 ##第一个特征置为1，即bias(偏差)
    for word in word_l:
        x[0, 1] += freqs.get((word, 1.), 0) ## 第二个特征是当前样本中积极词的词频
        x[0, 2] += freqs.get((word, 0.), 0) ## 第三个特征是当前样本中消极词的词频

    assert(x.shape == (1, 3))

    return x

测试一下特征提取的函数：

1
2
tmp = extract_features(train_x[0], freqs)
print(tmp)
[[1.00e+00 3.02e+03 6.10e+01]]

四、训练模型

  • 将所有样本的特征向量组合为矩阵X
  • 进行梯度下降
1
2
3
4
5
6
7
8
9
X = np.zeros((len(train_x), 3))
for i in range(len(train_x)):
    X[i, :] = extract_features(train_x[i], freqs)

Y = train_y

J, theta = gradient(X, Y, np.zeros((3, 1)), 1e-9, 6500)
print(f"训练后的损失为 {J}.")
print("训练后的权重向量为{}.".format(theta))
J1 [[0.1309]]
训练后的损失为 0.13089999889658352.
训练后的权重向量为[[ 2.78105442e-07]
 [ 1.08727164e-03]
 [-9.69515169e-04]].

五、测试所写逻辑回归分类器

预测一个推文是积极的还是消极的:

  • 处理推文，提取特征
  • 将特征输入到已经学习好权重参数的模型进行预测 \[y_{pred} = sigmoid(\mathbf{x} \cdot \theta)\]
1
2
3
4
5
def predict_tweet(tweet, freqs, theta):
    x = extract_features(tweet, freqs)
    y_pred = sigmoid(np.dot(x, theta))
#     print('y_pred', y_pred)
    return y_pred
1
2
def sentiment(x):
    return str('Good') if x>0.5 else str('Bad')
1
2
3
for tweet in ['I am happy', 'I am very pleasent', 'I am bad',
              'this movie should have been great.' ,'awful', 'It\'s wonderful']:
    print('{}-->{}-->{}'.format(tweet, float(predict_tweet(tweet, freqs, theta)), sentiment(float(predict_tweet(tweet, freqs, theta)))))
I am happy-->0.5393185864852428-->Good
I am very pleasent-->0.5000000695263604-->Good
I am bad-->0.4907181319136419-->Bad
this movie should have been great.-->0.5332393560274574-->Good
awful-->0.4932727475531824-->Bad
It's wonderful-->0.5048857705293124-->Good

算出分类准确度：

1
2
3
4
5
6
7
8
9
def test_lr(test_x, test_y, freqs, theta):
	y_hat = []

	for tweet in test_x:
		y_pred = predict_tweet(tweet, freqs, theta)
		y_hat.append(1) if y_pred > 0.5 else y_hat.append(0)

		accuracy = (y_hat==np.squeeze(test_y)).sum()/len(test_x)
		return accuracy
1
2
tmp_accuracy = test_lr(test_x, test_y, freqs, theta)
print(f"逻辑回归分类器模型的准确度为={tmp_accuracy:.4f}")
逻辑回归分类器模型的准确度为=0.9945