朴素贝叶斯分类器(Naive Bayes Classifiers)
0 准备知识
概率(Probability)：用于表示一件事情发生的可能性大小。有时，我们可以用一件事情发生的频率(实验做了很多很多次)来代表概率。(这个是频率派对概率的认识，当然还存在很多其他有不同的认识的派别)
条件概率(Conditional Probability)：用于表示一件事情(A)发生后另外一件事情(B)发生的概率，用\(P(B|A)\)。条件概率\(P(B|A)\)的计算可以用韦恩图来说明，在事件A发生了的情况下，那么B发生的可能性是A和B相交的面积除以A的面积。
用公式来表示即： \[ P(B|A) = \frac{P(A,B)}{P(A)} \]
1 朴素贝叶斯分类器简介
朴素贝叶斯分类器是一种对特征之间的相互影响做出了一定假设(这种假设让模型更简单，naive)的贝叶斯分类器。
朴素贝叶斯模型的直觉如下图所示： 
这是朴素贝叶斯分类器作用于一个影评，文字的顺序被忽略掉了(看成是bag of words)，利用的是每个字的频率。
朴素贝叶斯分类器属于概率型分类器，也就是对于文本d，分类器返回的是在给定文本的条件下后验概率最大对应的分类\(\hat{c}\)： 
贝叶斯分类就是利用 \(\color{purple}{贝叶斯规则}\) 将上面式子中的条件概率转换为其他形式。 \(\color{purple}{贝叶斯规则}\) 如下所示，它给出了将条件概率 \(P(x|y)\)表示为其他概率( \(P(x), P(y), P(y|x)\) )的方式： \[ P(x|y) = \frac{P(y|x)P(x)}{P(y)} \]
贝叶斯规则的推导(依据条件概率)：因为 \(P(x|y) = \frac{P(x,y)}{P(y)}\) 且 \(P(y|x) = \frac{P(x,y)}{P(x)}\) ，将后面的公式变形为： \(P(x,y) = P(y|x) \cdot P(x)\) ，带入前面的公式即为贝叶斯规则。
那么，朴素贝叶斯分类器的分类方程就变为：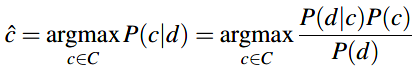 
对于上面式子中的分母 \(P(d)\) 可以省去，因为我们会在每个分类LZM上计算 \(\frac{P(d|c)P(c)}{P(d)}\)，对于每个分类 \(c\)，\(P(d)\)不会改变。所以分类方程就简化为：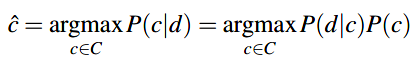 
所以，给定文本d通过选择两个概率：分类的先验概率 \(P(c)\) 和 该分类下文本的概率\(P(d|c)\) 的乘积最大的分类来确定输出：
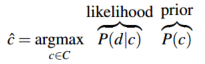
忽略一般化的损失，将文本d表示为特征的集合 \(f_1,f_2,\cdots,f_n\) :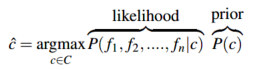 
上面的式子直接计算起来依旧比较困难，因为估计所有可能的特征组合(举例来说，每个可能的词和位置的集合)需要很多很多的参数还导致训练集特别大。基于此，朴素贝叶斯分类器做出了两个为了简化的假设：
1.假设文本中的词的位置不重要，即
bag of words。这个假设就是认为一个词，比如"love"，它出现在第1位或第20位或者是最后都是一样的。所以，朴素贝叶斯分类器假设了 \(f_1,f_2,\cdots,f_n\) 仅仅编码了词本身并没有位置信息。2.条件独立假设(也叫做朴素贝叶斯假设)：给定分类 \(c\) ,概率 \(P(f_i|c)\)是独立的。所以 \(P(f_1,f_2,\cdots,f_n|c)\)可以写成概率简单相乘的形式：
所以，朴素贝叶斯分类器的分类方程可以写为： 
为了将朴素贝叶斯分类器用于文本分类，可以简单地通过索引(index)遍历在某分类下的文本中的每个词来实现： 
其中，positions是当前的文本(句子)包含的所有词的位置。(如何用于分类见后面的例子)
为了避免出现很小(underflow导致)或者很大(increase speed导致)的值的出现，朴素贝叶斯的计算在对数空间进行，也就是取对数：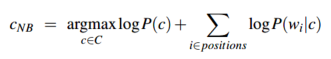 
通过取对数，朴素贝叶斯分类方程使用的是 \(\color{green}{输入(特征)的线性组合}\) (逻辑回归也是)，所以它属于线性分类器。
2 训练朴素贝叶斯分类器
通过第一部分知道了朴素贝叶斯的分类方程，那么如何计算概率 \(P(c)\) 和 \(P(f_i|c)\) 呢？
对于分类c的前验概率\(P(c)\)，可以通过分类c的样本数 \(N_c\) 占总样本数 \(N_total\) (训练集)的比例来估计，即： \[
\hat{P}(c) = \frac{N_c}{N_total}
\]
对于\(P(f_i|c)\)，假设特征就是样本中的词，所以此处便为\(P(w_i|c)\)，利用用词\(w_i\)在分类c出现的次数与所有词在分类c出现的次数之比来估计：
\(V\)是样本中所有的词。
举例来看\(P(w_i|c)\)的计算。假设训练集样本为： 
计算上述训练集对应的词\(P(w_i|c)\)： 
这样依次计算下去就可以把所有词的都计算出来。
这里有一个问题是，假如给定分类"positive"要估计"fantastic"的概率，但是训练集中"fantastic"没有出现在"positive"分类中，而"negative"中有，那么这个特征的概率将会是0：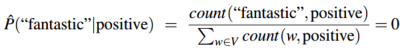 
因为朴素贝叶斯模型分类时将所有特征的概率相乘，所以整个句子属于分类c的概率将会是0，其余特征无法有效发挥其作用了。最简单的解决办法是Laplace(拉普拉斯)平滑，也就是分子分母同时加1： 
对于有些在测试集中出现，但是语料库中(训练集的)没有出现的词(unknown words)直接忽略掉它们，不参与计算。
在很多文本分类的应用中，去掉语料库中的stop word往往提高不了性能，所以更常见的是利用整个的语料库。
最后，整个的算法如下图所示： 
3 朴素贝叶斯用于分类的简单示例
这里利用简单的情感分类："positive"或"negative"来演示朴素贝叶斯算法。下面是训练和测试的样本，包括分类(Cat)和样本(Document): 
两个分类的前验概率为(\(\frac{N_c}{N_total}\))： \[ P(-) = \frac{3}{5} P(+) = \frac{2}{5} \]
看到测试集中的样本predictable with no fun，其中"with"没有出现在训练集中，所以忽略掉这个词。利用Laplace平滑可以计算得到： 
所以最后，测试集中的样本S = predictable with no fun，去除"with"后，计算分类的概率： 
可以利用上面两个式子的比值： \[ ratio = \frac{P(+)P(S|+)}{P(-)P(S|-)} = \frac{正样本数}{负样本数} \cdot \frac{正分类下的推文概率}{负分类下的推文概率} \] (公式还可以取对数) 如果大于1，则分类为"+"，如果小于1，则分类为"-"。
所以，该朴素贝叶斯模型预测的测试集样本S = predictable with no fun的分类是negative。