朴素贝叶斯分类器实现情感识别

利用逻辑回归分类器实现的博客在这里

任务描述

识别推文中的情感是积极的还是消极的。

给定一个推文： I am happy because I am learning NLP

现在，任务目标就是判断上面的推文是积极的情感(positive sentiment)还是消极的情感(nagetive sentiment)。

给定一个训练集，训练集中包含推文和其对应的标签(label)，标签取值为1(代表positive)和0(代表negative)。

任务数据集

NLTK语料库中的tweet数据集。

目录

  • 一、数据预处理
  • 二、训练朴素贝叶斯训练模型
  • 三、测试朴素贝叶斯模型

一、数据预处理

1.1 预处理文本

1 stop words 和 punctuation(标点)

在提取特征前，需要去除stop words，因为stop words通常是没有意义的词语，例如下图中的stop words表，这只是其中很小的一部分(对当前例子来说完全足够)。有时候文本中的punctuation(标点)对任务没有影响，这时就可以根据punctuation表来去除标点。

去除stop words
去除标点符号

去除stop words和punctuation后的文本还有可能包含句柄或url，对于情感识别任务，句柄或url没有影响，所以可以去除。

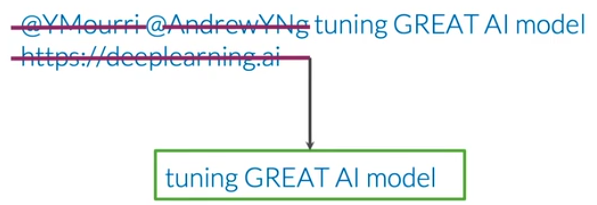
如果某任务中标点符号具有重要信息或者价值，就不用去除标点符号。

2 Stemming(词干提取) 和 lowercasing(小写化)

词干提取(stemming)可以减少统计同一词语的不同形式，词汇量能够大大减少。小写化所有词能够统一词语。

经过上述处理最后得到的推文为:[tun, great, ai, model]。

1.2 代码

导入包 

1
2
3
4
5
6
7
8
9
10
11
12
13
import pdb
import nltk
from nltk.corpus import twitter_samples
import numpy as np
import pandas as pd
import string
from nltk.tokenize import TweetTokenizer
from nltk.stem import PorterStemmer
from nltk.corpus import stopwords
import re

%matplotlib inline
%config InlineBackend.figure_format='svg'
划分训练样本和测试样本

1
2
3
4
5
6
7
8
9
10
11
12
13
all_positive_tweets = twitter_samples.strings('positive_tweets.json')
all_negative_tweets = twitter_samples.strings('negative_tweets.json')

# 划分训练和测试数据
train_pos = all_positive_tweets[:4000]
test_pos = all_positive_tweets[4000:]
train_neg = all_negative_tweets[:4000]
test_neg = all_negative_tweetsp[4000:]

train_x = train_pos + train_neg
test_x = test_pos + test_neg
train_y = np.append(np.ones(len(train_pos)), np.zeros(len(train_neg)))
test_y = np.append(np.ones(len(test_pos)), np.zeros(len(test_neg)))

1 处理数据

首先去除数据中的噪声——没有含义的词，比如说'I, you, are, is, etc...'，并不能对情感给出信息。然后是一些转发符、超链接、标签(话题标签的符号)等一些对识别情感没有作用的数据。最后对样本去除标点符号以及主干提取。见下面的process_tweet函数。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def process_tweet(tweet):
    stemmer=PorterStemmer()
    stopwords_english=stopwords.words('english')
    
    # remove stock market tickers like $GE
    tweet = re.sub(r'\$\w*', '', tweet)
    # remove old style retweet text "RT"
    tweet = re.sub(r'^RT[\s]+', '', tweet)
    # remove hyperlinks
    tweet = re.sub(r'https?:\/\/.*[\r\n]*', '', tweet)
    # remove hashtags
    # only removing the hash # sign from the word
    tweet = re.sub(r'#', '', tweet)
    
    tokenizer=TweetTokenizer(preserve_case=False,strip_handles=True,
                             reduce_len=True)
    
    tweet_tokens=tokenizer.tokenize(tweet)
    
    tweets_clean=[]
    
    for word in tweet_tokens:
        if word not in stopwords_english\
         and word not in string.punctuation:
            stem_word=stemmer.stem(word)
            tweets_clean.append(stem_word)
            
    return tweets_clean
2 创建键值对为{(词-类别):次数}的字典

利用朴素贝叶斯模型进行分类需要知道词在某类别中出现的次数。举个简单的例子，假设训练集为：['i am happy', 'i am tricked', 'i am sad', 'i am tired', 'i am tired']，样本分类对应[1, 0, 0, 0, 0]，那么其中出现的词在1和0这两个类别下的次数为：{('happi', 1): 1, ('trick', 0): 1, ('sad', 0): 1, ('tire', 0): 2}。(注意："i"和"am"被处理掉了。)

1
2
3
4
5
6
7
8
9
10
def count_tweets(result, tweets, ys):
    # result一般传进来空的字典：{}
    for y, tweet in zip(ys, tweets):
        for word in process_tweet(tweet):
            pair = (word, y)
            if pair in result:
                result[pair] += 1
            else:
                result[pair] = 1
    return result

二、训练朴素贝叶斯训练模型

关于朴素贝叶斯算法见另一篇博客传动门。

首先需要计算出每个分类的概率。\(P(D_{pos})\)是推文为"positive"的概率，\(P(D_{neg})\)是推文为"negative"的概率，那么： \[P(D_{pos}) = \frac{D_{pos}}{D}\tag{1}\]

\[P(D_{neg}) = \frac{D_{neg}}{D}\tag{2}\] 其中，\(D\)是全部推文的样本数，\(D_{pos}\)是"positive"的样本数，\(D_{neg}\) 是"negative"的样本数。

接着来计算Prior与Logprior。Prior=\(\frac{P(D_{pos})}{P(D_{neg})}\)，它代表一个推文是积极的(positive)还是消极的(negative)的概率，也就是说我们随机从训练集中选择一条推文，那么它是积极的可能性高还是消极的可能性高呢？这就可以由Prior看出来。Prior可以取对数，即为logprior: \[\text{logprior} = log \left( \frac{P(D_{pos})}{P(D_{neg})} \right) = log \left( \frac{D_{pos}}{D_{neg}} \right)\]

由对数性质可以简化为： \[\text{logprior} = \log (P(D_{pos})) - \log (P(D_{neg})) = \log (D_{pos}) - \log (D_{neg})\]

最后来计算推文中每个词W在"positive"和"negative"中出现的概率(也就是频率，用次数来计算)： \[ P(W_{pos}) = \frac{freq_{pos} + 1}{N_{pos} + V}\tag{4} \] \[ P(W_{neg}) = \frac{freq_{neg} + 1}{N_{neg} + V}\tag{5} \]

其中，\(freq_{pos}\)和{freq_{neg}分别是每个词对应的频率字典，上一节中所计算的字典。N_{pos}是所有标签为"positive"也就是1的词的数量，N_{neg}是所有标签为"negative"也就是0的词的数量。这样就可以计算出推文的正分类和负分类概率的比例，取对数为：\(log \left( \frac{P(W_{pos})}{P(W_{neg})} \right)\)。

1
freqs = count_tweets({}, train_x, train_y) ## 计算分类频率字典
1
2
3
4
5
6
7
8
9
def lookup(freqs, word, label):
	"""
	用于获取分类频率字典中(word, label)出现的次数n
	"""
	n = 0
	pair = (word, label)
	if pair in freqs:
		n = freqs[pair]
	return n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def train_naive_bayes(freqs, train_x, trian_y):
	loglikelihood = {}
	logprior = 0

	## 计算V，即vocab语料库(不含重复的词)中词的数量
	vocab = set([pair[0] for pair in freqs.keys()])
	V = len(vocab)

	## 计算N_pos，所有标签为"positive"也就是1的词的数量；以及N_neg，所有标签为"negative"也就是0的词的数量
	N_pos = 0
	N_neg = 0
	for pair in freqs.keys():
		if pair[1] == 1:
			N_pos += freqs[pair]
		else:
			N_neg += freqs[pair]

	## 计算D_pos与D_neg，正样本数和负样本数
	D_pos = (len(list(filter(lambda x:x>0, train_y)))) ## 过滤掉label为0的就是label为1的样本数
	D_neg = (len(list(filter(lambda x:x<=0, train_y))))

	## 计算logprior
	logprior = np.log(D_pos) - np.log(D_neg)

	for word in vocab:
		## 计算词的正负分类下的次数
		freq_pos = lookup(freqs, word, 1)
		freq_neg = lookup(freqs, word, 0)

		## 计算每个词的正负分类下的概率
		p_w_pos = (freq_pos+1) / (N_pos+V)
		P_w_neg = (freq_neg+1) / (N_neg+V)

		## 计算正负分类下概率的比值的对数
		loglikelihood[word] = np.log(p_w_pos/p_w_neg)
	return logprior, loglikelihood

计算logprior和loglikelihood 

1
2
3
logprior, loglikelihood = train_naive_bayes(freqs, train_x, train_y)
print(logprior)
print(loglikelihood)
因为这里label为1和label为0的数据是一样多的，所以logprior为0，尽管如此我们也要把这项保留着，进行一般性的流程，因为一般情况下，这个比值不为1。

三、测试朴素贝叶斯模型

利用上面小节计算的logprior和loglikelihood来预测推文啦！对于某一条推文，计算它分类的概率： \[ p = logprior + \sum_i^N (loglikelihood_i)\]

预测函数： 

1
2
3
4
5
6
7
8
9
def naive_bayes_predict(tweet, logprior, loglikelihood):
	word_l = process_tweet(tweet)
	p = 0

	p += logprior
	for word in word_l:
		if word in loglikelihood:
			p += loglikelihood[word]
	return p
1
2
3
4
## 测试预测函数
my_tweet = 'She smiled.'
p = naive_bayes_predict(my_tweet, logprior, loglikelihood)
print('The expected output is', p)
预测函数的输出>0时，预测此样本为正样本"positive"；预测输出<0时，预测此样本为负样本"negative"。

检查预测结果的准确度： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def test_naive_bayes(test_x, test_y, logprior, loglikelihood):
	accuracy = 0
	y_hats = []

	for tweet in test_x:
		if naive_bayes_predict(tweet, logprior, loglikelihood)>0:
			y_hat_i = 1
		else:
			y_hat_i = 0
		y_hats.append(y_hat_i)

	error = np.mean(np.absolute(y_hats - test_y))
	accuracy = 1 - error

	return accuracy
1
2
## 输出模型预测的准确度
print("Naive Bayes accuracy = {.4f}".format(test_naive_bayes(test_x, test_y, logprior, loglikelihood)))