幸福感预测

本案例基于天池大赛上的：“快来一起挖掘幸福感”，比赛链接：传送门

1 赛题背景

在社会科学领域，幸福感的研究占有重要的位置。这个涉及了哲学、心理学、社会学、经济学等多方学科的话题复杂而有趣；同时与大家生活息息相关，每个人对幸福感都有自己的衡量标准。如果能发现影响幸福感的共性，生活中是不是将多一些乐趣；如果能找到影响幸福感的政策因素，便能优化资源配置来提升国民的幸福感。目前社会科学研究注重变量的可解释性和未来政策的落地，主要采用了线性回归和逻辑回归的方法，在收入、健康、职业、社交关系、休闲方式等经济人口因素；以及政府公共服务、宏观经济环境、税负等宏观因素上有了一系列的推测和发现。

赛题尝试了幸福感预测这一经典课题，希望在现有社会科学研究外有其他维度的算法尝试，结合多学科各自优势，挖掘潜在的影响因素，发现更多可解释、可理解的相关关系。

2 赛题说明

赛题使用公开数据的问卷调查结果，选取其中多组变量来预测其对幸福感的评价，包括：

个体变量（性别、年龄、地域、职业、健康、婚姻与政治面貌等等）；
家庭变量（父母、配偶、子女、家庭资本等等）；
社会态度（公平、信用、公共服务等等）。

幸福感预测的准确性不是赛题的唯一目的，更希望对变量间的关系、变量群的意义有所探索与收获。

3 数据说明

考虑到变量个数较多、部分变量间关系复杂，数据分为完整版和精简版两类。可从精简版入手熟悉赛题后，使用完整版挖掘更多信息。

complete文件为变量完整版数据，abbr文件为变量精简版数据。完整的数据变量拥有139维的特征，共有8000组的训练样本用于幸福感预测(幸福感的值为：1, 2, 3, 4, 5，其中1代表幸福感最弱，5代表幸福感最强)

index文件中包含每个变量对应的问卷题目，以及变量取值的含义。

survey文件是数据源的原版问卷，作为补充以方便理解问题背景。

数据来源：赛题使用的数据来自中国人民大学中国调查与数据中心主持之《中国综合社会调查（CGSS）》项目。赛题感谢此机构及其人员提供数据协助。中国综合社会调查为多阶分层抽样的截面面访调查。

外部数据：赛题以数据挖掘和分析为出发点，不限制外部数据的使用，比如宏观经济指标、政府再分配政策等公开数据。

4 评测指标

提交结果为csv文件，其中包含id和happiness的预测值两列。

根据真实值和提交结果中的happiness的预测值来计算得分score: \[ score = \frac{1}{n}\sum_{n=1}^n (y_i - y^{*})^2 \] 其中，\(n\)代表测试集样本数量，\(y_i\)代表第i个测试样本的预测值，\(y^*\)代表该测试样本的真实值。

5 案例分析和解决方案

5.1 导入项目所用包

import os
import time 
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
from datetime import datetime
import matplotlib.pyplot as plt
from sklearn.metrics import roc_auc_score, roc_curve, mean_squared_error,mean_absolute_error, f1_score
import lightgbm as lgb
import xgboost as xgb
from sklearn.ensemble import RandomForestRegressor as rfr
from sklearn.ensemble import ExtraTreesRegressor as etr
from sklearn.linear_model import BayesianRidge as br
from sklearn.ensemble import GradientBoostingRegressor as gbr
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import LinearRegression as lr
from sklearn.linear_model import ElasticNet as en
from sklearn.kernel_ridge import KernelRidge as kr
from sklearn.model_selection import  KFold, StratifiedKFold,GroupKFold, RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn import preprocessing
import logging
import warnings

warnings.filterwarnings('ignore') #消除warning

5.2 导入数据集

数据导入与观察：

1
2
3

train = pd.read_csv("train.csv", parse_dates=['survey_time'], encoding='latin-1') #latin-1向下兼容ASCII
test = pd.read_csv("test.csv", parse_dates=['survey_time'], encoding='latin-1')
train.describe()

数据的目标值分割：

train = train[train['happiness']!=-8].reset_index(drop=True) ## 删除"happiness" 为-8的行
train_data_copy = train.copy()
target_col = 'happiness'
target = train_data_copy[target_col]
del train_data_copy[target_col]

data = pd.concat([train_data_copy, test], axis=0, ignore_index=True)

### 5.3 数据预处理

首先需要对于数据中连续出现的负数值进行处理。由于数据中的负数值只有：-1、-2、-3、-8这几种数值，所以对它们分别进行操作，实现代码如下：

#数据中有负数值：-1、-2、-3、-8，将他们视为有问题的特征，但是不删去
def getres1(row):
	return len([x for x in row.values if type(x) == int and x < 0])
def getres2(row):
	return len([x for x in row.values if type(x) == int and x == -8])
def getres3(row):
	return len([x for x in row.values if type(x) == int and x == -1])
def getres4(row):
	return len([x for x in row.values if type(x) == int and x == -2])
def getres5(row):
	return len([x for x in row.values if type(x) == int and x == -3])

# 检查数据
data['neg1'] =  data[data.columns].apply(lambda row:getres1(row), axis=1)
data.loc[data['neg1']>20, 'neg1'] = 20 ## 平滑处理
data['neg2'] = data[data.columns].apply(lambda row:getres2(row), aixs=1)
data['neg3'] = data[data.columns].apply(lambda row:getres3(row),axis=1)
data['neg4'] = data[data.columns].apply(lambda row:getres4(row),axis=1)
data['neg5'] = data[data.columns].apply(lambda row:getres5(row),axis=1)

接下来进行填充缺失值。在这里采取的方式是将缺失值补全，利用函数fillna(value)，其中value的数值根据具体的情况来定，例如：将大部分的缺失信息认为是0，将家庭成员数的缺失值填充为1，将家庭收入这个特征的缺失值填充为66365(即所有家庭的收入平均值)。

#填充缺失值 共25列 去掉4列 填充21列

#以下的列都是缺省的，根据它们自己的情况进行填补

data['work_status'] = data['work_status'].fillna(0)
data['work_yr'] = data['work_yr'].fillna(0)
data['work_manage'] = data['work_manage'].fillna(0)
data['work_type'] = data['work_type'].fillna(0)

data['edu_yr'] = data['edu_yr'].fillna(0)
data['edu_status'] = data['edu_status'].fillna(0)

data['s_work_type'] = data['s_work_type'].fillna(0)
data['s_work_status'] = data['s_work_status'].fillna(0)
data['s_political'] = data['s_political'].fillna(0)
data['s_hukou'] = data['s_hukou'].fillna(0)
data['s_income'] = data['s_income'].fillna(0)
data['s_birth'] = data['s_birth'].fillna(0)
data['s_edu'] = data['s_edu'].fillna(0)
data['s_work_exper'] = data['s_work_exper'].fillna(0)

data['minor_child'] = data['minor_child'].fillna(0)
data['marital_now'] = data['marital_now'].fillna(0)
data['marital_1st'] = data['marital_1st'].fillna(0)
data['social_neighbor']=data['social_neighbor'].fillna(0)
data['social_friend']=data['social_friend'].fillna(0)
data['hukou_loc']=data['hukou_loc'].fillna(1) #最少为1，表示户口
data['family_income']=data['family_income'].fillna(66365) #删除问题值后的平均值

除了上面的处理，还有特殊格式的信息需要另外处理，比如时间。然后还要基于已有的出生日期和调查时间进行年龄的计算和年龄的分层。

data['survey_time'] = pd.to_datatime(data['survey_time'], format='%y-%m-%d', errors='coerce')  #防止时间格式不同的报错errors='coerce'
data['survey_time'] = data['suyvey_time'].dt.year ## 仅仅保留年份，方便计算年龄
data['age'] = data['survey_time'] - data['birth']

bins = [0, 17, 26, 34, 50, 63, 100]
data['age_bin'] = pd.cut(data['age'], bins, labels=[0, 1, 2, 3, 4, 5])

对于有些特征的缺失值补全，可以采用的其他方式就是根据日常生活中的真实情况主观地进行补全。例如“宗教信息”特征为负数的认为是“不信仰宗教”，并认为“参加宗教活动的频率”为1，即没有参加过宗教活动。

#对‘宗教’处理
data.loc[data['religion']<0,'religion'] = 1 #1为不信仰宗教
data.loc[data['religion_freq']<0,'religion_freq'] = 1 #1为从来没有参加过
#对‘教育程度’处理
data.loc[data['edu']<0,'edu'] = 4 #初中
data.loc[data['edu_status']<0,'edu_status'] = 0
data.loc[data['edu_yr']<0,'edu_yr'] = 0
#对‘个人收入’处理
data.loc[data['income']<0,'income'] = 0 #认为无收入
#对‘政治面貌’处理
data.loc[data['political']<0,'political'] = 1 #认为是群众
#对体重处理（个人想法）
data.loc[(data['weight_jin']<=80)&(data['height_cm']>=160),'weight_jin']= data['weight_jin']*2
data.loc[data['weight_jin']<=60,'weight_jin']= data['weight_jin']*2
#对身高处理
data.loc[data['height_cm']<150,'height_cm'] = 150 #成年人的实际情况
#对‘健康’处理
data.loc[data['health']<0,'health'] = 4 #认为是比较健康
data.loc[data['health_problem']<0,'health_problem'] = 4
#对‘沮丧’处理
data.loc[data['depression']<0,'depression'] = 4 #一般人都是很少吧
#对‘媒体’处理
data.loc[data['media_1']<0,'media_1'] = 1 #都是从不
data.loc[data['media_2']<0,'media_2'] = 1
data.loc[data['media_3']<0,'media_3'] = 1
data.loc[data['media_4']<0,'media_4'] = 1
data.loc[data['media_5']<0,'media_5'] = 1
data.loc[data['media_6']<0,'media_6'] = 1
#对‘空闲活动’处理
data.loc[data['leisure_1']<0,'leisure_1'] = 1 #根据自己的想法
data.loc[data['leisure_2']<0,'leisure_2'] = 5
data.loc[data['leisure_3']<0,'leisure_3'] = 3
data.loc[data['socialize']<0,'socialize'] = 2 #很少

data.loc[data['relax']<0,'relax'] = 4 #经常
data.loc[data['learn']<0,'learn'] = 1 #从不
#对‘社交’处理
data.loc[data['social_neighbor']<0,'social_neighbor'] = 0
data.loc[data['social_friend']<0,'social_friend'] = 0
data.loc[data['socia_outing']<0,'socia_outing'] = 1
data.loc[data['neighbor_familiarity']<0,'social_neighbor']= 4
#对‘社会公平性’处理
data.loc[data['equity']<0,'equity'] = 4
#对‘社会等级’处理
data.loc[data['class_10_before']<0,'class_10_before'] = 3
data.loc[data['class']<0,'class'] = 5
data.loc[data['class_10_after']<0,'class_10_after'] = 5
data.loc[data['class_14']<0,'class_14'] = 2
#对‘工作情况’处理
data.loc[data['work_status']<0,'work_status'] = 0
data.loc[data['work_yr']<0,'work_yr'] = 0
data.loc[data['work_manage']<0,'work_manage'] = 0
data.loc[data['work_type']<0,'work_type'] = 0
#对‘社会保障’处理
data.loc[data['insur_1']<0,'insur_1'] = 1
data.loc[data['insur_2']<0,'insur_2'] = 1
data.loc[data['insur_3']<0,'insur_3'] = 1
data.loc[data['insur_4']<0,'insur_4'] = 1
data.loc[data['insur_1']==0,'insur_1'] = 0
data.loc[data['insur_2']==0,'insur_2'] = 0
data.loc[data['insur_3']==0,'insur_3'] = 0
data.loc[data['insur_4']==0,'insur_4'] = 0

有的情况利用众数对缺失值进行处理会更加合理，使用众数函数mode()（来实现异常值的修正）。

data.loc[data['leisure_4']<0,'leisure_4'] = data['leisure_4'].mode() #取众数
data.loc[data['leisure_5']<0,'leisure_5'] = data['leisure_5'].mode()
data.loc[data['leisure_6']<0,'leisure_6'] = data['leisure_6'].mode()
data.loc[data['leisure_7']<0,'leisure_7'] = data['leisure_7'].mode()
data.loc[data['leisure_8']<0,'leisure_8'] = data['leisure_8'].mode()
data.loc[data['leisure_9']<0,'leisure_9'] = data['leisure_9'].mode()
data.loc[data['leisure_10']<0,'leisure_10'] = data['leisure_10'].mode()
data.loc[data['leisure_11']<0,'leisure_11'] = data['leisure_11'].mode()
data.loc[data['leisure_12']<0,'leisure_12'] = data['leisure_12'].mode()

取均值进行缺失值的补全（代码实现为means()），在这里因为家庭的收入是连续值，所以不能再使用取众数的方法进行处理，这里就直接使用了均值进行缺失值的补全。

1 2	family_income_mean = data['family_income'].mean() data.loc[data['family_income']<0,'family_income'] = family_income_mean

其他缺失值处理：

#对家庭情况处理
data.loc[data['family_m']<0,'family_m'] = 2
data.loc[data['family_status']<0,'family_status'] = 3
data.loc[data['house']<0,'house'] = 1
data.loc[data['car']<0,'car'] = 0
data.loc[data['car']==2,'car'] = 0 #变为0和1
data.loc[data['son']<0,'son'] = 1
data.loc[data['daughter']<0,'daughter'] = 0
data.loc[data['minor_child']<0,'minor_child'] = 0
#对‘婚姻’处理
data.loc[data['marital_1st']<0,'marital_1st'] = 0
data.loc[data['marital_now']<0,'marital_now'] = 0
#对‘配偶’处理
data.loc[data['s_birth']<0,'s_birth'] = 0
data.loc[data['s_edu']<0,'s_edu'] = 0
data.loc[data['s_political']<0,'s_political'] = 0
data.loc[data['s_hukou']<0,'s_hukou'] = 0
data.loc[data['s_income']<0,'s_income'] = 0
data.loc[data['s_work_type']<0,'s_work_type'] = 0
data.loc[data['s_work_status']<0,'s_work_status'] = 0
data.loc[data['s_work_exper']<0,'s_work_exper'] = 0
#对‘父母情况’处理
data.loc[data['f_birth']<0,'f_birth'] = 1945
data.loc[data['f_edu']<0,'f_edu'] = 1
data.loc[data['f_political']<0,'f_political'] = 1
data.loc[data['f_work_14']<0,'f_work_14'] = 2
data.loc[data['m_birth']<0,'m_birth'] = 1940
data.loc[data['m_edu']<0,'m_edu'] = 1
data.loc[data['m_political']<0,'m_political'] = 1
data.loc[data['m_work_14']<0,'m_work_14'] = 2
#和同龄人相比社会经济地位
data.loc[data['status_peer']<0,'status_peer'] = 2
#和3年前比社会经济地位
data.loc[data['status_3_before']<0,'status_3_before'] = 2
#对‘观点’处理
data.loc[data['view']<0,'view'] = 4
#对期望年收入处理
data.loc[data['inc_ability']<=0,'inc_ability']= 2
inc_exp_mean = data['inc_exp'].mean()
data.loc[data['inc_exp']<=0,'inc_exp']= inc_exp_mean #取均值

#部分特征处理，取众数（首先去除缺失值的数据）
for i in range(1,9+1):
    data.loc[data['public_service_'+str(i)]<0,'public_service_'+str(i)] = data['public_service_'+str(i)].dropna().mode().values
for i in range(1,13+1):
    data.loc[data['trust_'+str(i)]<0,'trust_'+str(i)] = data['trust_'+str(i)].dropna().mode().values

5.4 数据增广

为了更好地利用数据，需要进一步地分析，进行数据增广。通过分析每一个特征之间的关系，进行新特征的增加，比如：第一次结婚年龄、最近结婚年龄、是否再婚、配偶年龄、配偶年龄差、各种收入比（与配偶之间的收入比、十年后预期收入与现在收入之比等等）、收入与住房面积比（其中也包括10年后期望收入等等各种情况）、社会阶级（10年后的社会阶级、14年后的社会阶级等等）、悠闲指数、满意指数、信任指数等等。

除此之外，还考虑了同一省市内的收入的平均值等以及一个个体相对于同省、市、县其他人的各个指标的情况。同时也考虑了对于同龄人之间的相互比较，即在同龄人中的收入情况、健康情况等等。

#第一次结婚年龄 147
data['marital_1stbir'] = data['marital_1st'] - data['birth'] 
#最近结婚年龄 148
data['marital_nowtbir'] = data['marital_now'] - data['birth'] 
#是否再婚 149
data['mar'] = data['marital_nowtbir'] - data['marital_1stbir']
#配偶年龄 150
data['marital_sbir'] = data['marital_now']-data['s_birth']
#配偶年龄差 151
data['age_'] = data['marital_nowtbir'] - data['marital_sbir'] 

#收入比 151+7 =158
data['income/s_income'] = data['income']/(data['s_income']+1) #同居伴侣
data['income+s_income'] = data['income']+(data['s_income']+1)
data['income/family_income'] = data['income']/(data['family_income']+1)
data['all_income/family_income'] = (data['income']+data['s_income'])/(data['family_income']+1)
data['income/inc_exp'] = data['income']/(data['inc_exp']+1)
data['family_income/m'] = data['family_income']/(data['family_m']+0.01)
data['income/m'] = data['income']/(data['family_m']+0.01)

#收入/面积比 158+4=162
data['income/floor_area'] = data['income']/(data['floor_area']+0.01)
data['all_income/floor_area'] = (data['income']+data['s_income'])/(data['floor_area']+0.01)
data['family_income/floor_area'] = data['family_income']/(data['floor_area']+0.01)
data['floor_area/m'] = data['floor_area']/(data['family_m']+0.01)

#class 162+3=165
data['class_10_diff'] = (data['class_10_after'] - data['class'])
data['class_diff'] = data['class'] - data['class_10_before']
data['class_14_diff'] = data['class'] - data['class_14']

#悠闲指数 166
leisure_fea_lis = ['leisure_'+str(i) for i in range(1,13)]
data['leisure_sum'] = data[leisure_fea_lis].sum(axis=1) #skew
#满意指数 167
public_service_fea_lis = ['public_service_'+str(i) for i in range(1,10)]
data['public_service_sum'] = data[public_service_fea_lis].sum(axis=1) #skew

#信任指数 168
trust_fea_lis = ['trust_'+str(i) for i in range(1,14)]
data['trust_sum'] = data[trust_fea_lis].sum(axis=1) #skew

#province mean 168+13=181
data['province_income_mean'] = data.groupby(['province'])['income'].transform('mean').values
data['province_family_income_mean'] = data.groupby(['province'])['family_income'].transform('mean').values
data['province_equity_mean'] = data.groupby(['province'])['equity'].transform('mean').values
data['province_depression_mean'] = data.groupby(['province'])['depression'].transform('mean').values
data['province_floor_area_mean'] = data.groupby(['province'])['floor_area'].transform('mean').values
data['province_health_mean'] = data.groupby(['province'])['health'].transform('mean').values
data['province_class_10_diff_mean'] = data.groupby(['province'])['class_10_diff'].transform('mean').values
data['province_class_mean'] = data.groupby(['province'])['class'].transform('mean').values
data['province_health_problem_mean'] = data.groupby(['province'])['health_problem'].transform('mean').values
data['province_family_status_mean'] = data.groupby(['province'])['family_status'].transform('mean').values
data['province_leisure_sum_mean'] = data.groupby(['province'])['leisure_sum'].transform('mean').values
data['province_public_service_sum_mean'] = data.groupby(['province'])['public_service_sum'].transform('mean').values
data['province_trust_sum_mean'] = data.groupby(['province'])['trust_sum'].transform('mean').values

#city   mean 181+13=194
data['city_income_mean'] = data.groupby(['city'])['income'].transform('mean').values #按照city分组
data['city_family_income_mean'] = data.groupby(['city'])['family_income'].transform('mean').values
data['city_equity_mean'] = data.groupby(['city'])['equity'].transform('mean').values
data['city_depression_mean'] = data.groupby(['city'])['depression'].transform('mean').values
data['city_floor_area_mean'] = data.groupby(['city'])['floor_area'].transform('mean').values
data['city_health_mean'] = data.groupby(['city'])['health'].transform('mean').values
data['city_class_10_diff_mean'] = data.groupby(['city'])['class_10_diff'].transform('mean').values
data['city_class_mean'] = data.groupby(['city'])['class'].transform('mean').values
data['city_health_problem_mean'] = data.groupby(['city'])['health_problem'].transform('mean').values
data['city_family_status_mean'] = data.groupby(['city'])['family_status'].transform('mean').values
data['city_leisure_sum_mean'] = data.groupby(['city'])['leisure_sum'].transform('mean').values
data['city_public_service_sum_mean'] = data.groupby(['city'])['public_service_sum'].transform('mean').values
data['city_trust_sum_mean'] = data.groupby(['city'])['trust_sum'].transform('mean').values

#county  mean 194 + 13 = 207
data['county_income_mean'] = data.groupby(['county'])['income'].transform('mean').values
data['county_family_income_mean'] = data.groupby(['county'])['family_income'].transform('mean').values
data['county_equity_mean'] = data.groupby(['county'])['equity'].transform('mean').values
data['county_depression_mean'] = data.groupby(['county'])['depression'].transform('mean').values
data['county_floor_area_mean'] = data.groupby(['county'])['floor_area'].transform('mean').values
data['county_health_mean'] = data.groupby(['county'])['health'].transform('mean').values
data['county_class_10_diff_mean'] = data.groupby(['county'])['class_10_diff'].transform('mean').values
data['county_class_mean'] = data.groupby(['county'])['class'].transform('mean').values
data['county_health_problem_mean'] = data.groupby(['county'])['health_problem'].transform('mean').values
data['county_family_status_mean'] = data.groupby(['county'])['family_status'].transform('mean').values
data['county_leisure_sum_mean'] = data.groupby(['county'])['leisure_sum'].transform('mean').values
data['county_public_service_sum_mean'] = data.groupby(['county'])['public_service_sum'].transform('mean').values
data['county_trust_sum_mean'] = data.groupby(['county'])['trust_sum'].transform('mean').values

#ratio 相比同省 207 + 13 =220
data['income/province'] = data['income']/(data['province_income_mean'])                                      
data['family_income/province'] = data['family_income']/(data['province_family_income_mean'])   
data['equity/province'] = data['equity']/(data['province_equity_mean'])       
data['depression/province'] = data['depression']/(data['province_depression_mean'])                                                
data['floor_area/province'] = data['floor_area']/(data['province_floor_area_mean'])
data['health/province'] = data['health']/(data['province_health_mean'])
data['class_10_diff/province'] = data['class_10_diff']/(data['province_class_10_diff_mean'])
data['class/province'] = data['class']/(data['province_class_mean'])
data['health_problem/province'] = data['health_problem']/(data['province_health_problem_mean'])
data['family_status/province'] = data['family_status']/(data['province_family_status_mean'])
data['leisure_sum/province'] = data['leisure_sum']/(data['province_leisure_sum_mean'])
data['public_service_sum/province'] = data['public_service_sum']/(data['province_public_service_sum_mean'])
data['trust_sum/province'] = data['trust_sum']/(data['province_trust_sum_mean']+1)

#ratio 相比同市 220 + 13 =233
data['income/city'] = data['income']/(data['city_income_mean'])                                      
data['family_income/city'] = data['family_income']/(data['city_family_income_mean'])   
data['equity/city'] = data['equity']/(data['city_equity_mean'])       
data['depression/city'] = data['depression']/(data['city_depression_mean'])                                                
data['floor_area/city'] = data['floor_area']/(data['city_floor_area_mean'])
data['health/city'] = data['health']/(data['city_health_mean'])
data['class_10_diff/city'] = data['class_10_diff']/(data['city_class_10_diff_mean'])
data['class/city'] = data['class']/(data['city_class_mean'])
data['health_problem/city'] = data['health_problem']/(data['city_health_problem_mean'])
data['family_status/city'] = data['family_status']/(data['city_family_status_mean'])
data['leisure_sum/city'] = data['leisure_sum']/(data['city_leisure_sum_mean'])
data['public_service_sum/city'] = data['public_service_sum']/(data['city_public_service_sum_mean'])
data['trust_sum/city'] = data['trust_sum']/(data['city_trust_sum_mean'])

#ratio 相比同个地区 233 + 13 =246
data['income/county'] = data['income']/(data['county_income_mean'])                                      
data['family_income/county'] = data['family_income']/(data['county_family_income_mean'])   
data['equity/county'] = data['equity']/(data['county_equity_mean'])       
data['depression/county'] = data['depression']/(data['county_depression_mean'])                                                
data['floor_area/county'] = data['floor_area']/(data['county_floor_area_mean'])
data['health/county'] = data['health']/(data['county_health_mean'])
data['class_10_diff/county'] = data['class_10_diff']/(data['county_class_10_diff_mean'])
data['class/county'] = data['class']/(data['county_class_mean'])
data['health_problem/county'] = data['health_problem']/(data['county_health_problem_mean'])
data['family_status/county'] = data['family_status']/(data['county_family_status_mean'])
data['leisure_sum/county'] = data['leisure_sum']/(data['county_leisure_sum_mean'])
data['public_service_sum/county'] = data['public_service_sum']/(data['county_public_service_sum_mean'])
data['trust_sum/county'] = data['trust_sum']/(data['county_trust_sum_mean'])

#age   mean 246+ 13 =259
data['age_income_mean'] = data.groupby(['age'])['income'].transform('mean').values
data['age_family_income_mean'] = data.groupby(['age'])['family_income'].transform('mean').values
data['age_equity_mean'] = data.groupby(['age'])['equity'].transform('mean').values
data['age_depression_mean'] = data.groupby(['age'])['depression'].transform('mean').values
data['age_floor_area_mean'] = data.groupby(['age'])['floor_area'].transform('mean').values
data['age_health_mean'] = data.groupby(['age'])['health'].transform('mean').values
data['age_class_10_diff_mean'] = data.groupby(['age'])['class_10_diff'].transform('mean').values
data['age_class_mean'] = data.groupby(['age'])['class'].transform('mean').values
data['age_health_problem_mean'] = data.groupby(['age'])['health_problem'].transform('mean').values
data['age_family_status_mean'] = data.groupby(['age'])['family_status'].transform('mean').values
data['age_leisure_sum_mean'] = data.groupby(['age'])['leisure_sum'].transform('mean').values
data['age_public_service_sum_mean'] = data.groupby(['age'])['public_service_sum'].transform('mean').values
data['age_trust_sum_mean'] = data.groupby(['age'])['trust_sum'].transform('mean').values

# 和同龄人相比259 + 13 =272
data['income/age'] = data['income']/(data['age_income_mean'])                                      
data['family_income/age'] = data['family_income']/(data['age_family_income_mean'])   
data['equity/age'] = data['equity']/(data['age_equity_mean'])       
data['depression/age'] = data['depression']/(data['age_depression_mean'])                                                
data['floor_area/age'] = data['floor_area']/(data['age_floor_area_mean'])
data['health/age'] = data['health']/(data['age_health_mean'])
data['class_10_diff/age'] = data['class_10_diff']/(data['age_class_10_diff_mean'])
data['class/age'] = data['class']/(data['age_class_mean'])
data['health_problem/age'] = data['health_problem']/(data['age_health_problem_mean'])
data['family_status/age'] = data['family_status']/(data['age_family_status_mean'])
data['leisure_sum/age'] = data['leisure_sum']/(data['age_leisure_sum_mean'])
data['public_service_sum/age'] = data['public_service_sum']/(data['age_public_service_sum_mean'])
data['trust_sum/age'] = data['trust_sum']/(data['age_trust_sum_mean'])

经过如上的操作后，最终我们的特征从一开始的131维，扩充为了272维的特征。

1	print('shape',data.shape)

输出：shape (10956, 272)

对于有效样本数很少的特征，例如负值太多的特征或者是缺失值太多的特征，进行删除。一共删除了包括“目前的最高教育程度”在内的9类特征，得到了最终的263维的特征。

#删除数值特别少的和之前用过的特征
del_list=['id','survey_time','edu_other','invest_other','property_other','join_party','province','city','county']
use_feature = [clo for clo in data.columns if clo not in del_list]
data.fillna(0,inplace=True) #还是补0
train_shape = train.shape[0] #一共的数据量，训练集
features = data[use_feature].columns #删除后所有的特征
X_train_263 = data[:train_shape][use_feature].values
y_train = target
X_test_263 = data[train_shape:][use_feature].values
X_train_263.shape #最终一种263个特征

输出：(7988, 263)

这里选择了最重要的49个特征，作为除了以上263维特征外的另外一组特征。

imp_fea_49 = ['equity','depression','health','class','family_status','health_problem','class_10_after',
           'equity/province','equity/city','equity/county',
           'depression/province','depression/city','depression/county',
           'health/province','health/city','health/county',
           'class/province','class/city','class/county',
           'family_status/province','family_status/city','family_status/county',
           'family_income/province','family_income/city','family_income/county',
           'floor_area/province','floor_area/city','floor_area/county',
           'leisure_sum/province','leisure_sum/city','leisure_sum/county',
           'public_service_sum/province','public_service_sum/city','public_service_sum/county',
           'trust_sum/province','trust_sum/city','trust_sum/county',
           'income/m','public_service_sum','class_diff','status_3_before','age_income_mean','age_floor_area_mean',
           'weight_jin','height_cm',
           'health/age','depression/age','equity/age','leisure_sum/age'
          ]
train_shape = train.shape[0]
X_train_49 = data[:train_shape][imp_fea_49].values
X_test_49 = data[train_shape:][imp_fea_49].values
X_train_49.shape #最重要的49个特征

输出：(7988, 49)

选择需要进行onehot编码的离散变量进行one-hot编码，再合成为第三类特征，共383维。

cat_fea = ['survey_type','gender','nationality','edu_status','political','hukou','hukou_loc','work_exper','work_status','work_type',
           'work_manage','marital','s_political','s_hukou','s_work_exper','s_work_status','s_work_type','f_political','f_work_14',
           'm_political','m_work_14'] #已经是0、1的值不需要onehot
noc_fea = [clo for clo in use_feature if clo not in cat_fea]

onehot_data = data[cat_fea].values
enc = preprocessing.OneHotEncoder(categories = 'auto')
oh_data=enc.fit_transform(onehot_data).toarray()
oh_data.shape #变为onehot编码格式

X_train_oh = oh_data[:train_shape,:]
X_test_oh = oh_data[train_shape:,:]
X_train_oh.shape #其中的训练集

X_train_383 = np.column_stack([data[:train_shape][noc_fea].values,X_train_oh])#先是noc，再是cat_fea
X_test_383 = np.column_stack([data[train_shape:][noc_fea].values,X_test_oh])
X_train_383.shape

输出：(7988, 383)

基于此，我们构建完成了三种特征工程（训练数据集），其一是上面提取的最重要的49中特征，其中包括健康程度、社会阶级、在同龄人中的收入情况等等特征。其二是扩充后的263维特征（这里可以认为是初始特征）。其三是使用One-hot编码后的特征，这里要使用One-hot进行编码的原因在于，有部分特征为分离值，例如性别中男女，男为1，女为2，我们想使用One-hot将其变为男为0，女为1，来增强机器学习算法的鲁棒性能；再如民族这个特征，原本是1-56这56个数值，如果直接分类会让分类器的鲁棒性变差，所以使用One-hot编码将其变为6个特征进行非零即一的处理。

5.5 特征建模

对于263维的特征

1. lightGBM

首先我们对于原始的263维的特征，使用lightGBM进行处理，这里使用5折交叉验证的方法：

#lightGBM决策树
lgb_263_param = {
'num_leaves': 7, 
'min_data_in_leaf': 20, #叶子可能具有的最小记录数
'objective':'regression',
'max_depth': -1,
'learning_rate': 0.003,
"boosting": "gbdt", #用gbdt算法
"feature_fraction": 0.18, #例如 0.18时，意味着在每次迭代中随机选择18％的参数来建树
"bagging_freq": 1,
"bagging_fraction": 0.55, #每次迭代时用的数据比例
"bagging_seed": 14,
"metric": 'mse',
"lambda_l1": 0.1,
"lambda_l2": 0.2, 
"verbosity": -1}
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=4)   #交叉切分：5
oof_lgb_263 = np.zeros(len(X_train_263))
predictions_lgb_263 = np.zeros(len(X_test_263))

for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):

    print("fold n°{}".format(fold_+1))
    trn_data = lgb.Dataset(X_train_263[trn_idx], y_train[trn_idx])
    val_data = lgb.Dataset(X_train_263[val_idx], y_train[val_idx])#train:val=4:1

    num_round = 10000
    lgb_263 = lgb.train(lgb_263_param, trn_data, num_round, valid_sets = [trn_data, val_data], verbose_eval=500, early_stopping_rounds = 800)
    oof_lgb_263[val_idx] = lgb_263.predict(X_train_263[val_idx], num_iteration=lgb_263.best_iteration)
    predictions_lgb_263 += lgb_263.predict(X_test_263, num_iteration=lgb_263.best_iteration) / folds.n_splits

print("CV score: {:<8.8f}".format(mean_squared_error(oof_lgb_263, target)))

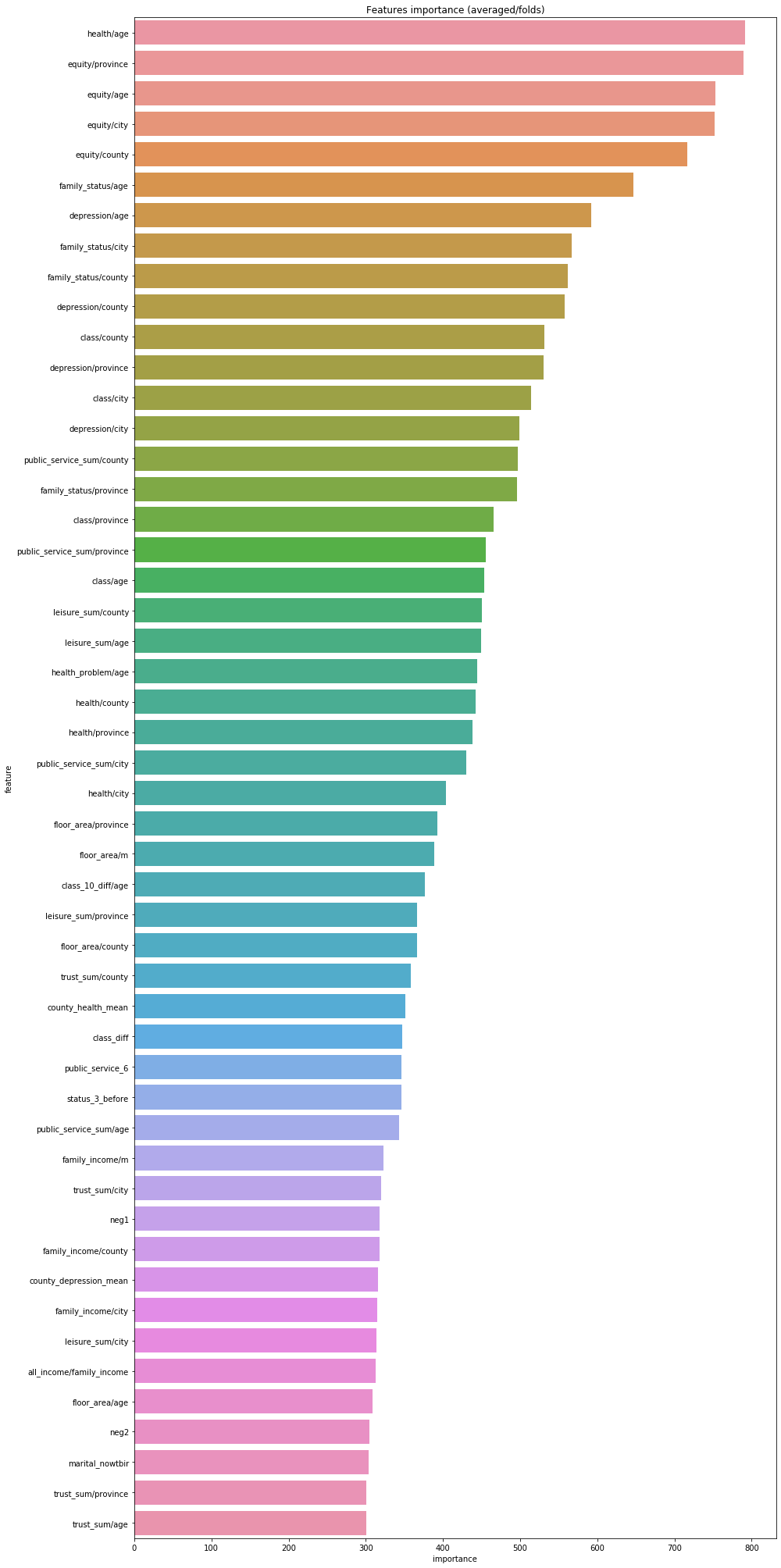
使用已经训练完的lightGBM的模型进行特征重要性的判断以及可视化。

#---------------特征重要性
pd.set_option('display.max_columns', None)
#显示所有行
pd.set_option('display.max_rows', None)
#设置value的显示长度为100，默认为50
pd.set_option('max_colwidth',100)
df = pd.DataFrame(data[use_feature].columns.tolist(), columns=['feature'])
df['importance']=list(lgb_263.feature_importance())
df = df.sort_values(by='importance',ascending=False)
plt.figure(figsize=(14,28))
sns.barplot(x="importance", y="feature", data=df.head(50))
plt.title('Features importance (averaged/folds)')
plt.tight_layout()

2. xgboost

#xgboost
xgb_263_params = {'eta': 0.02,  #lr
              'max_depth': 6,  
              'min_child_weight':3,#最小叶子节点样本权重和
              'gamma':0, #指定节点分裂所需的最小损失函数下降值。
              'subsample': 0.7,  #控制对于每棵树，随机采样的比例
              'colsample_bytree': 0.3,  #用来控制每棵随机采样的列数的占比 (每一列是一个特征)。
              'lambda':2,
              'objective': 'reg:linear', 
              'eval_metric': 'rmse', 
              'silent': True, 
              'nthread': -1}


folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=2019)
oof_xgb_263 = np.zeros(len(X_train_263))
predictions_xgb_263 = np.zeros(len(X_test_263))

for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
    print("fold n°{}".format(fold_+1))
    trn_data = xgb.DMatrix(X_train_263[trn_idx], y_train[trn_idx])
    val_data = xgb.DMatrix(X_train_263[val_idx], y_train[val_idx])

    watchlist = [(trn_data, 'train'), (val_data, 'valid_data')]
    xgb_263 = xgb.train(dtrain=trn_data, num_boost_round=3000, evals=watchlist, early_stopping_rounds=600, verbose_eval=500, params=xgb_263_params)
    oof_xgb_263[val_idx] = xgb_263.predict(xgb.DMatrix(X_train_263[val_idx]), ntree_limit=xgb_263.best_ntree_limit)
    predictions_xgb_263 += xgb_263.predict(xgb.DMatrix(X_test_263), ntree_limit=xgb_263.best_ntree_limit) / folds.n_splits

print("CV score: {:<8.8f}".format(mean_squared_error(oof_xgb_263, target)))

3. RandomForest 随机森林

#RandomForestRegressor随机森林
folds = KFold(n_splits=5, shuffle=True, random_state=2019)
oof_rfr_263 = np.zeros(len(X_train_263))
predictions_rfr_263 = np.zeros(len(X_test_263))

for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
    print("fold n°{}".format(fold_+1))
    tr_x = X_train_263[trn_idx]
    tr_y = y_train[trn_idx]
    rfr_263 = rfr(n_estimators=1600,max_depth=9, min_samples_leaf=9, min_weight_fraction_leaf=0.0,
            max_features=0.25,verbose=1,n_jobs=-1) #并行化
    #verbose = 0 为不在标准输出流输出日志信息
#verbose = 1 为输出进度条记录
#verbose = 2 为每个epoch输出一行记录
    rfr_263.fit(tr_x,tr_y)
    oof_rfr_263[val_idx] = rfr_263.predict(X_train_263[val_idx])
    
    predictions_rfr_263 += rfr_263.predict(X_test_263) / folds.n_splits

print("CV score: {:<8.8f}".format(mean_squared_error(oof_rfr_263, target)))

4. GradientBoostingDecisionTree 梯度提升决策树

#GradientBoostingRegressor梯度提升决策树
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=2018)
oof_gbr_263 = np.zeros(train_shape)
predictions_gbr_263 = np.zeros(len(X_test_263))

for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
    print("fold n°{}".format(fold_+1))
    tr_x = X_train_263[trn_idx]
    tr_y = y_train[trn_idx]
    gbr_263 = gbr(n_estimators=400, learning_rate=0.01,subsample=0.65,max_depth=7, min_samples_leaf=20,
            max_features=0.22,verbose=1)
    gbr_263.fit(tr_x,tr_y)
    oof_gbr_263[val_idx] = gbr_263.predict(X_train_263[val_idx])
    
    predictions_gbr_263 += gbr_263.predict(X_test_263) / folds.n_splits

print("CV score: {:<8.8f}".format(mean_squared_error(oof_gbr_263, target)))

5. ExtraTree 极端随机森林回归

#ExtraTreesRegressor 极端随机森林回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_etr_263 = np.zeros(train_shape)
predictions_etr_263 = np.zeros(len(X_test_263))

for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
    print("fold n°{}".format(fold_+1))
    tr_x = X_train_263[trn_idx]
    tr_y = y_train[trn_idx]
    etr_263 = etr(n_estimators=1000,max_depth=8, min_samples_leaf=12, min_weight_fraction_leaf=0.0,
            max_features=0.4,verbose=1,n_jobs=-1)# max_feature：划分时考虑的最大特征数
    etr_263.fit(tr_x,tr_y)
    oof_etr_263[val_idx] = etr_263.predict(X_train_263[val_idx])
    
    predictions_etr_263 += etr_263.predict(X_test_263) / folds.n_splits

print("CV score: {:<8.8f}".format(mean_squared_error(oof_etr_263, target)))

至此，我们得到了以上5种模型的预测结果以及模型架构及参数。其中在每一种特征工程中，进行5折的交叉验证，并重复两次（Kernel Ridge Regression，核脊回归），取得每一个特征数下的模型的结果。

train_stack2 = np.vstack([oof_lgb_263,oof_xgb_263,oof_gbr_263,oof_rfr_263,oof_etr_263]).transpose()
# transpose()函数的作用就是调换x,y,z的位置,也就是数组的索引值
test_stack2 = np.vstack([predictions_lgb_263, predictions_xgb_263,predictions_gbr_263,predictions_rfr_263,predictions_etr_263]).transpose()

#交叉验证:5折，重复2次
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack2 = np.zeros(train_stack2.shape[0])
predictions_lr2 = np.zeros(test_stack2.shape[0])

for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack2,target)):
    print("fold {}".format(fold_))
    trn_data, trn_y = train_stack2[trn_idx], target.iloc[trn_idx].values
    val_data, val_y = train_stack2[val_idx], target.iloc[val_idx].values
    #Kernel Ridge Regression
    lr2 = kr()
    lr2.fit(trn_data, trn_y)
    
    oof_stack2[val_idx] = lr2.predict(val_data)
    predictions_lr2 += lr2.predict(test_stack2) / 10
    
mean_squared_error(target.values, oof_stack2)

接下来对49维的特征数据和383维的特征数据进行上述263维特征数据相同的操作。

5.6 网格搜索进行参数调整

from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
 
iris = load_iris()
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=0)
print("Size of training set:{} size of testing set:{}".format(X_train.shape[0],X_test.shape[0]))
 
####   1
best_score = 0
for gamma in [0.001,0.01,0.1,1,10,100]:
    for C in [0.001,0.01,0.1,1,10,100]:
        svm = SVC(gamma=gamma,C=C)#对于每种参数可能的组合，进行一次训练；
        svm.fit(X_train,y_train)
        score = svm.score(X_test,y_test)
        if score > best_score:#找到表现最好的参数
            best_score = score
            best_parameters = {'gamma':gamma,'C':C}
print("Best score:{:.2f}".format(best_score))

 

####   2
from sklearn.model_selection import GridSearchCV
 
#把要调整的参数以及其候选值 列出来；
param_grid = {"gamma":[0.001,0.01,0.1,1,10,100],
             "C":[0.001,0.01,0.1,1,10,100]}
print("Parameters:{}".format(param_grid))
 
grid_search = GridSearchCV(SVC(),param_grid,cv=5) #实例化一个GridSearchCV类,cv交叉验证参数
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=10)
grid_search.fit(X_train,y_train) #训练，找到最优的参数，同时使用最优的参数实例化一个新的SVC estimator。
print("Test set score:{:.2f}".format(grid_search.score(X_test,y_test)))
print("Best parameters:{}".format(grid_search.best_params_))

#SVM模型有两个非常重要的参数C与gamma。
#C是惩罚系数，即对误差的容忍度（间隔大小,分类准确度）。C越高，说明越不能容忍出现误差,容易过拟合。C越小，容易欠拟合。C过大或过小，泛化能力变差
#gamma是选择RBF函数作为kernel后，该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多。支持向量的个数影响训练与预测的速度。
#两者独立

Result:
    
Parameters:{'gamma': [0.001, 0.01, 0.1, 1, 10, 100], 'C': [0.001, 0.01, 0.1, 1, 10, 100]}
Test set score:0.97
Best parameters:{'C': 10, 'gamma': 0.1}
Best score on train set:0.98

#Grid Search 调参方法存在的共性弊端就是：耗时；参数越多，候选值越多，耗费时间越长！所以，一般情况下，先定一个大范围，然后再细化。