堆

1 什么是堆？

堆是一种有自己规则的树，分为最大堆和最小堆。堆从上往下数值增加或者减小，分别对应最小堆和最大堆。

最大堆：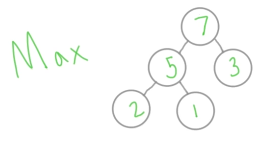

最小堆：

堆不仅仅可以是二叉树，还可以是多叉树。但它得是完全(complete)树(除了倒数第一层外，其余层需要完全填充)。不同类型的树，堆的搜索、插入、删除有很大的不同。

下面以最大堆(完全二叉树)为例来看堆的操作。

2 堆的搜索

从堆头开始，依次往下比较。

放一个简单的最大堆在这，并在最大堆中搜索2：

这种情况属于最差的情况，需要搜索整颗树。所以最差时间复杂度是O(n)。

如果在最大堆中搜索8，那么直接在堆头就可以返回结果：没有。因为堆头为最大值，而8大于堆头。这种情况属于最好的情况，时间复杂度为O(1)。

如果在最大堆中搜索6，情况如下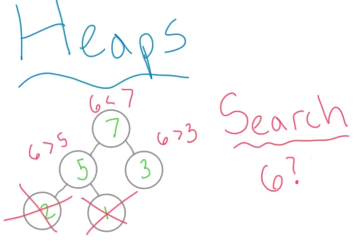： 搜索一半左右的节点后发现它大于某个节点的值，那么便不用往下再去搜索了，因为当前节点的值大于其孩子节点的值。这种情况属于平均情况，时间大约是O(n/2)，也就是O(n)。

3 python实现堆

3.1 利用heapq模块

实际上，虽然python中没有独立的堆模块，但是拥有包含堆操作函数的模块：heapq，其中堆相关的函数为：

函数 解释
heappush(heap, x) 将x压入堆中
heappop(heap) 弹出堆顶元素
heapify(heap) 让列表heap具备堆特征
heapreplace(heap, x) 弹出堆顶元素，并将x压入堆中

注意：heapq模块默认的堆是最小堆。如果需要最大堆，使用一个转换的trick就好。

  • 最小堆示例：
1
2
3
4
5
from heapq import *
heap = [20, 2, 3, 1, 7, 5, 4]
heapify(heap) ## heap被转化为最小堆
heappush(heap, 8) ## 向heap中增加元素8
min_heap = heappop(heap) ## 弹出最小堆的堆顶元素（即最小值）
  • 最大堆示例：
1
2
3
4
5
6
from heapq import *
heap = [20, 2, 3, 1, 7, 5, 4]
heap_max = []
for item in heap:
    heappush(heap_max, (-item, item)) ## 用元素的相反数建最小堆就对应了元素本身的最大堆
_, max_value = heappop(heap_max) ## max_value即为弹出的堆顶元素（元素最大值）

3.2 自己实现堆结构

因为python提供的list实际上是一个线性表（Array），但因为

4 LeetCode编程题

4.1 数据流中的中位数(295)

题目链接：https://leetcode-cn.com/problems/find-median-from-data-stream/

  • 题目内容

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

例如，

[2,3,4]的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

  • void addNum(int num) - 从数据流中添加一个整数到数据结构中。
  • double findMedian() - 返回目前所有元素的中位数。

示例： 

1
2
3
4
5
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3) 
findMedian() -> 2
进阶:

如果数据流中所有整数都在 0 到 100 范围内，你将如何优化你的算法？ 如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

  • python解法

本题参考题解：推荐一个很好的思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#
# @lc app=leetcode.cn id=295 lang=python3
#
# [295] 数据流的中位数
#

# @lc code=start
from heapq import *
class MedianFinder:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.size = 0
        self.minheap = []
        self.maxheap = []
        ## 普通解法
        # self.array = []


    def addNum(self, num: int) -> None:
        self.size += 1
        heappush(self.maxheap,(-num, num))
        _, maxheap_max = heappop(self.maxheap)
        heappush(self.minheap, maxheap_max)
        if self.size & 1: ## 奇数个数值时，保证最大堆多一个元素
            minheap_min = heappop(self.minheap)
            heappush(self.maxheap, (-minheap_min, minheap_min))
        # -------
        # 普通解法：
        # self.array.append(num)
        # self.array.sort()
        #-------

    def findMedian(self) -> float:
        if self.size & 1: ## 奇数个数值时
            median = self.maxheap[0][1]
            return median
        else:
            median = (self.maxheap[0][1]+self.minheap[0])/2
            return median
        # -------
        # 普通解法：
        # mid = len(self.array)//2
        # if len(self.array) % 2 != 0:
        #     return self.array[mid]
        # else:
        #     return (self.array[mid-1]+self.array[mid])/2
        # ------

# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()
# @lc code=end