字符串

收录字符的相关编程。

1 打印一个字符串全部子序列，包括空字符串

python实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
## 给定字符串s,找出它所有的子序列
def sub_string(s):
    result = []
    tmp = []
    process(s, 0, tmp, result)
    return result

## 给定字符串s，对于当前位置i，进行一个选择和不选择。当前的结果是tmp，所有结果集合为result
def process(s, i, tmp, result):
    if i == len(s):
        result.append(''.join(tmp))
        return
    ## 选择当前字符
    tmp.append(s[i])
    process(s, i+1, tmp[:], result)
    ## 不选择当前字符
    tmp.pop()
    process(s, i+1, tmp[:], result)
    
print('final',sub_string('abcs'))
```  
    
## 2 两个字符串的最长公共子序列

部分对应LeetCode题目：1143

python实现：

```python
## 求最长公共子序列的长度
def longestCommonSubsequence(text1: str, text2: str, dp) -> int:
    m, n = len(text1), len(text2)
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if text1[i - 1] == text2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

    return dp[-1][-1]

## 求出最长公共子序列，在dp数组的遍历方式可以参考下面的图
def trace_back(text1, text2, i, j, dp, tmp, s):
    
    while i > 0 and j > 0:
        if text1[i-1] == text2[j-1]:
            tmp.insert(0, (text1[i-1]))
            i -= 1
            j -= 1
        else:
            if dp[i-1][j] > dp[i][j-1]:
                i -= 1
            elif dp[i-1][j] < dp[i][j-1]:
                j -= 1
            else:
                trace_back(text1, text2, i-1, j, dp, tmp[:], s)
                trace_back(text1, text2, i, j-1, dp, tmp[:], s)
                return
    s.append(''.join(tmp))
        
text1= 'ABCBDAB'
text2='BDCABA'
dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]
print(longestCommonSubsequence(text1, text2, dp))
s = []
trace_back(text1, text2, len(text1), len(text2), dp, [], s)
print('最长公共子串的集合：', s)

求出最长公共子序列，在dp数组的遍历方式可以参考下面的图：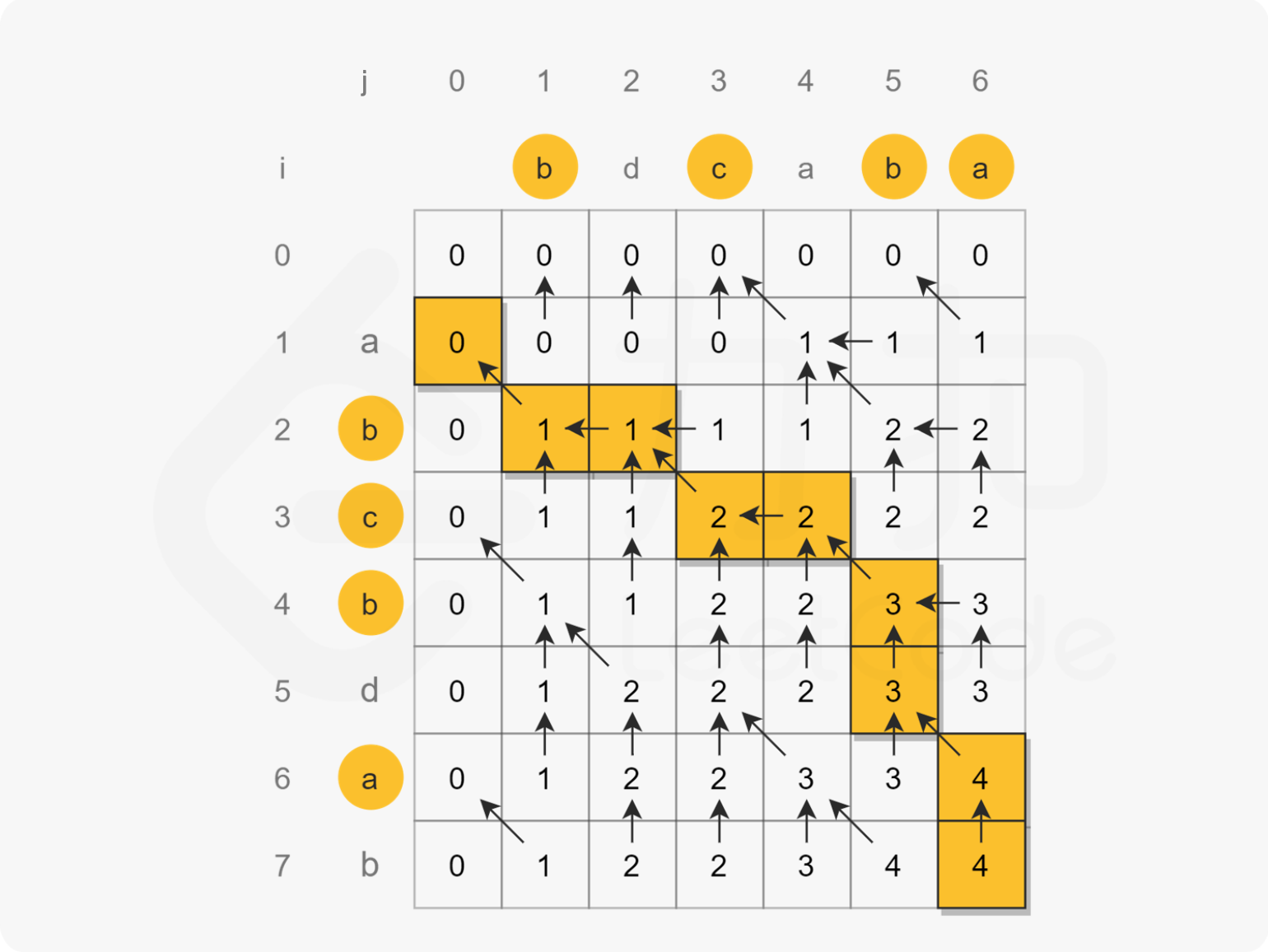

要是求两个字符串的公共子串，代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def longestCommonSubsting(text1: str, text2: str) -> int:
    m, n = len(text1), len(text2)
    dp = [[0]*(n+1) for _ in range(m+1)]
    max_length = 0
    max_index = -1
    for i in range(1, m + 1):
        for j in range(1, n + 1):
        	## 对应字符相同
            if text1[i - 1] == text2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
                if dp[i][j] > max_length:
                    max_length = dp[i][j]
                    if max_length == 1:
                        max_index = i - 1
            else: ## 对应字符不同
                dp[i][j] = 0
    return max_length, text1[max_index:max_index+max_length]
         
## 方法测试   
text1= 'ABCBDAB'
text2='BDCABA'
print(longestCommonSubstring(text1, text2))

3 字符串的所有排列组合

给定一个字符串，找出所有的其中字符的组合。

python实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
## 求所有的字符组合
def all_permutation(s, i, result):
    if i == len(s):
        result.append(''.join(s))
        return
    for j in range(i, len(s)):
        swap(s, i, j)
        all_permutation(s[:], i+1, result)
        swap(s, i, j)
def swap(s, i, j):
    tmp = s[i]
    s[i] = s[j]
    s[j] = tmp
 

## 测试
result= []
s = 'abc'
s = list(s)
all_permutation(s, 0, result)
print(result)
## 4 KMP——判断一个字符串是否为另一字符串的子串

KMP算法是对暴力匹配的一种优化/提升。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def get_next_array(str_target):
    next = [0 for i in range(len(str_target))]
    next[0] = -1
    i = 2
    pos = next[1]
    while i < len(str_target):
        if str_target[i] == str_target[pos]:
            next[i] = next[pos]+1
            i += 1
            pos = i-1
        elif i == 0:
            next[i] = 0
            pos = i-1
        else:
            pos = next[pos]
    return next
def KMP(str1, str2):
    if len(str2) > len(str1):
        return -1
    next = get_next_array(str2)
    head = -1
    i = 0
    j = 0
    flag = True
    while i < len(str1) and j < len(str2):
        if str1[i] == str2[j]: 
            if flag:
                head = i
                flag = False
            i += 1
            j += 1
        elif j == 0: ## 没法往前跳
            i += 1
            flag = True
        else: ## 失配，可以往前跳
            next_j = next[j]
            j = next_j
            head = i - next_j
            flag = False
    return head

# print(KMP("abcdascddfgfa", "cdd"))
print(KMP("abcdascddfggfga", "zzf"))